
斯坦福大学机器学习第六课"逻辑回归“学习笔记,本次课程主要包括7部分:
1) Classification(分类)
2) Hypothesis Representation
3) Decision boundary(决策边界)
4) Cost function(代价函数,成本函数)
5) Simplified cost function and gradient descent(简化版代价函数及梯度下降算法)
6) Advanced optimization(其他优化算法)
7) Multi-class classification: One-vs-all(多类分类问题)
以下是每一部分的详细解读。
1) Classification(分类)
分类问题举例:
- 邮件:垃圾邮件/非垃圾邮件?
- 在线交易:是否欺诈(是/否)?
- 肿瘤:恶性/良性?
以上问题可以称之为二分类问题,可以用如下形式定义:
其中0称之为负例,1称之为正例。
对于多分类问题,可以如下定义因变量y:

如果分类器用的是回归模型,并且已经训练好了一个模型,可以设置一个阈值:
- 如果
 ,则预测y=1,既y属于正例;
,则预测y=1,既y属于正例; - 如果
 ,则预测y=0,既y属于负例;
,则预测y=0,既y属于负例;
如果是线性回归模型,对于肿瘤这个二分类问题,图形表示如下:
但是对于二分类问题来说,线性回归模型的Hypothesis输出值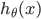 可以大于1也可以小于0。
可以大于1也可以小于0。
这个时候我们引出逻辑回归,逻辑回归的Hypothesis输出介于0与1之间,既:

注: 以下引自李航博士《统计学习方法》1.8节关于分类问题的一点描述:
分类是监督学习的一个核心问题,在监督学习中,当输出变量Y取有限个离散值时,预测问题便成为分类问题。这时,输入变量X可以是离散的,也可以是连续的。监督学习从数据中学习一个分类模型或分类决策函数,称为分类器(classifier)。分类器对新的输入进行输出的预测(prediction),称为分类(classification).
2) Hypothesis Representation
逻辑回归模型:
上一节谈到,我们需要将Hypothesis的输出界定在0和1之间,既:

但是线性回归无法做到,这里我们引入一个函数g, 令逻辑回归的Hypothesis表示为:

这里g称为Sigmoid function或者Logistic function, 具体表达式为:

Sigmoid 函数在有个很漂亮的“S"形,如下图所示(引自维基百科):
综合上述两式,我们得到逻辑回归模型的数学表达式:

其中 是参数。
是参数。
Hypothesis输出的直观解释:
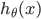 = 对于给定的输入x,y=1时估计的概率
= 对于给定的输入x,y=1时估计的概率
例如,对于肿瘤(恶性/良性),如果输入变量(特征)是肿瘤的大小:
这里Hypothesis表示的是”病人的肿瘤有70%的可能是恶性的“。
较正式的说法可以如下表示:
给定输入x,参数化的 (参数空间), y=1时的概率。
(参数空间), y=1时的概率。
数学上可以如下表示:

对于因变量y=0或1这样的二分类问题:


3) Decision boundary(决策边界)
如上节所述,逻辑回归模型可以如下表示:
假设给定的阈值是0.5,当 时, y = 1;
时, y = 1;
当 时,y = 0;
时,y = 0;
再次回顾sigmoid function的图形,也就是g(z)的图形:
当 时,
时,  ;
;
对于 , 则
, 则 , 此时意味着预估y=1;
, 此时意味着预估y=1;
反之,当预测y = 0时, ;
;
我们可以认为 = 0是一个决策边界,当它大于0或小于0时,逻辑回归模型分别预测不同的分类结果。例如,
= 0是一个决策边界,当它大于0或小于0时,逻辑回归模型分别预测不同的分类结果。例如,

 分别取-3, 1, 1,
分别取-3, 1, 1,
则当 时, y = 1; 则
时, y = 1; 则 是一个决策边界,图形表示如下:
是一个决策边界,图形表示如下:
上述只是一个线性的决策边界,当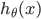 更复杂的时候,我们可以得到非线性的决策边界,例如:
更复杂的时候,我们可以得到非线性的决策边界,例如:
这里当 时,y=1,决策边界是一个圆形,如下图所示:
时,y=1,决策边界是一个圆形,如下图所示:
更复杂的例子,请参考官方PPT,这里就不再举例了。
4) Cost function(代价函数,成本函数)
逻辑回归概览:
逻辑回归是一种有监督的学习方法,因此有训练集:
对于这m个训练样本来说,每个样本都包含n+1个特征:
其中 ,
,  .
.
Hypothesis可表示为:

与线性回归相似,我们的问题是如何选择合适的参数 ?
?
Cost Function:
线性回归的Cost Function定义为:

这里可以把 简写为
简写为 ,更简化的表达式为:
,更简化的表达式为:

如果和线性回归相似,这里取  ,会存在一个问题,也就是逻辑回归的Cost Function是“非凸”的,如下图所示:
,会存在一个问题,也就是逻辑回归的Cost Function是“非凸”的,如下图所示:
我们知道,线性回归的Cost Function是凸函数,具有碗状的形状,而凸函数具有良好的性质:对于凸函数来说局部最小值点即为全局最小值点,因此只要能求得这类函数的一个最小值点,该点一定为全局最小值点。
因此,上述的Cost Function对于逻辑回归是不可行的,我们需要其他形式的Cost Function来保证逻辑回归的成本函数是凸函数。
这里补充一段李航博士《统计学习方法》里关于Cost Function或者损失函数(loss function)的说明,大家就可以理解Cost Function不限于一种方式,而是有多种方式可选,以下摘自书中的1.3.2小节:
监督学习问题是在假设空间F中选取模型f作为决策函数,对于给定的输入X,由f(X)给出相应的输出Y,这个输出的预测值f(X)与真实值Y可能一致也可能不一致,用一个损失函数(loss function)或代价函数(cost function)来度量预测错误的程度。损失函数是f(X)和Y的非负实值函数,记作L(Y, f(X)).
统计学习中常用的损失函数有以下几种:
(1) 0-1损失函数(0-1 loss function):
(2) 平方损失函数(quadratic loss function)
(3) 绝对损失函数(absolute loss function)
(4) 对数损失函数(logarithmic loss function) 或对数似然损失函数(log-likelihood loss function)
损失函数越小,模型就越好。
逻辑回归的Cost Function:
基于上节的描述和补充,这里我们选择对数似然损失函数作为逻辑回归的Cost Function:
直观的来解释这个Cost Function,首先看当y=1的情况:
直观来看, 如果y = 1,  ,则Cost = 0,也就是预测的值和真实的值完全相等的时候Cost =0;
,则Cost = 0,也就是预测的值和真实的值完全相等的时候Cost =0;
但是,当 时,
时, 
直观来看,由于预测的结果南辕北辙:
如果 , 也就是预测
, 也就是预测 ,也就是y=1的概率是0,但是实际上y = 1
,也就是y=1的概率是0,但是实际上y = 1
因此对于这个学习算法给予一个很大的Cost的惩罚。
同理对于y=0的情况也适用:
5) Simplified cost function and gradient descent(简化版代价函数及梯度下降算法)
逻辑回归的Cost Function可以表示为:
由于y 只能等于0或1,所以可以将逻辑回归中的Cost function的两个公式合并,具体推导如下:
故逻辑回归的Cost function可简化为:
对于这个公式,这里稍微补充一点,注意中括号中的公式正是对逻辑回归进行最大似然估计中的最大似然函数,对于最大似然函数求最大值,从而得到参数(\theta !min_\theta J(\theta)
!min_\theta J(\theta) h_\theta(x)
h_\theta(x) \theta
\theta J(\theta)
J(\theta) J(\theta)
J(\theta) J(\theta)
J(\theta) h_\theta(x)
h_\theta(x) \theta
\theta h^{(i)}_\theta(x)$$,并且预测 y = i时的概率;
h^{(i)}_\theta(x)$$,并且预测 y = i时的概率;
对于一个新的输入变量x, 分别对每一个类进行预测,取概率最大的那个类作为分类结果:
参考资料:
李航博士《统计学习方法》
http://en.wikipedia.org/wiki/Sigmoid_function
http://en.wikipedia.org/wiki/Logistic_function
http://en.wikipedia.org/wiki/Loss_function
http://en.wikipedia.org/wiki/Conjugate_gradient_method
http://en.wikipedia.org/wiki/Quasi-Newton_method
http://en.wikipedia.org/wiki/BFGS_method
http://en.wikipedia.org/wiki/Limited-memory_BFGS




代价函数求导之后(1/m)去哪了?
[回复]