
2. 认识Beta/Dirichlet分布
2.1 魔鬼的游戏---认识Beta 分布
统计学就是猜测上帝的游戏,当然我们不总是有机会猜测上帝,运气不好的时候就得揣度魔鬼的心思。有一天你被魔鬼撒旦抓走了,撒旦说:”你们人类很聪明,而我是很仁慈的,和你玩一个游戏,赢了就可以走,否则把灵魂出卖给我。游戏的规则很简单,我有一个魔盒,上面有一个按钮,你每按一下按钮,就均匀的输出一个[0,1]之间的随机数,我现在按10下,我手上有10个数,你猜第7大的数是什么,偏离不超过0.01就算对。“ 你应该怎么猜呢?
从数学的角度抽象一下,上面这个游戏其实是在说随机变量$X_1,X_2,\cdots,X_n {\stackrel{\mathrm{iid}}{\sim}} Uniform(0,1)$,把这$n$ 个随机变量排序后得到顺序统计量 $X_{(1)},X_{(2)},\cdots, X_{(n)}$, 然后问 $X_{(k)}$ 的分布是什么。
对于不喜欢数学的同学而言,估计每个概率分布都是一个恶魔,那在概率统计学中,均匀分布应该算得上是潘多拉魔盒,几乎所有重要的概率分布都可以从均匀分布$Uniform(0,1)$中生成出来;尤其是在统计模拟中,所有统计分布的随机样本都是通过均匀分布产生的。
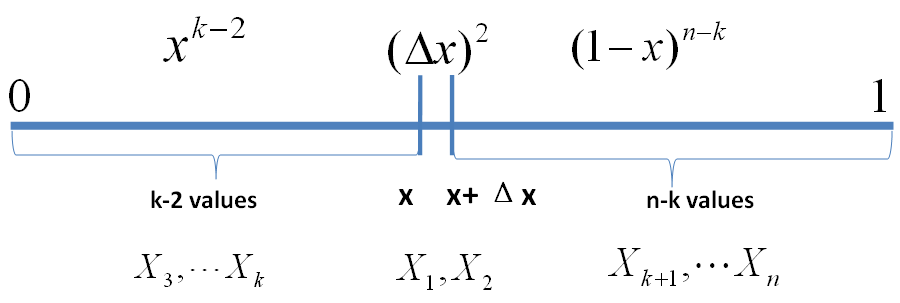
对于上面的游戏而言 $n=10,k=7$, 如果我们能求出 $X_{(7)}$ 的分布的概率密度,那么用概率密度的极值点去做猜测就是最好的策略。对于一般的情形,$X_{(k)}$ 的分布是什么呢?那我们尝试计算一下$X_{(k)}$ 落在一个区间 $[x, x+\Delta x]$ 的概率,也就是求如下概率值
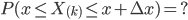
把 [0,1] 区间分成三段 $[0,x), [x,x+\Delta x], (x+\Delta x,1]$,我们先考虑简单的情形,假设$n$ 个数中只有一个落在了区间 $[x, x+\Delta x]$内,则因为这个区间内的数$X_{(k)}$是第$k$大的,则$[0,x)$中应该有 $k-1$ 个数,$(x,1]$ 这个区间中应该有$n-k$ 个数。不失一般性,我们先考虑如下一个符合上述要求的事件$E$
\begin{align*}
E = \{ & X_1 \in [x, x+\Delta x], \\
& X_i \in [0,x)\quad (i=2,\cdots,k), \\
& X_j \in (x+\Delta x,1] \quad (j=k+1,\cdots,n)\}
\end{align*}
则有
\begin{align*}
P(E) & = \prod_{i=1}^nP(X_i) \\
& = x^{k-1}(1-x-\Delta x)^{n-k}\Delta x \\
& = x^{k-1}(1-x)^{n-k}\Delta x + o(\Delta x)
\end{align*}
$o(\Delta x)$表示$\Delta x $的高阶无穷小。显然,由于不同的排列组合,即$n$个数中有一个落在 $[x, x+\Delta x]$区间的有$n$种取法,余下$n-1$个数中有$k-1$个落在$[0,x)$的有$\binom{n-1}{k-1}$种组合,所以和事件$E$等价的事件一共有 $n\binom{n-1}{k-1}$个。继续考虑稍微复杂一点情形,假设$n$ 个数中有两个数落在了区间 $[x, x+\Delta x]$,
\begin{align*}
E' = \{ & X_1,X_2\in [x, x+\Delta x], \\
& X_i \in [0,x) \quad (i=3,\cdots,k), \\
& X_j \in (x+\Delta x,1] \quad (j=k+1,\cdots,n)\}
\end{align*}
则有

从以上分析我们很容易看出,只要落在$[x, x+\Delta x]$内的数字超过一个,则对应的事件的概率就是 $o(\Delta x)$。于是
\begin{align*}
& P( x \le X_{(k)} \le x+\Delta x) \\
& = n\binom{n-1}{k-1}P(E) + o(\Delta x) \\
& = n\binom{n-1}{k-1}x^{k-1}(1-x)^{n-k}\Delta x + o(\Delta x)
\end{align*}
所以,可以得到$X_{(k)}$的概率密度函数为
\begin{align*}
f(x) & = \lim_{\Delta x \rightarrow 0} \frac{P( x \le X_{(k)} \le x+\Delta x)}{\Delta x} \\
& = n\binom{n-1}{k-1}x^{k-1}(1-x)^{n-k} \\
& = \frac{n!}{(k-1)!(n-k)!}x^{k-1}(1-x)^{n-k} \quad x \in [0,1]
\end{align*}
利用Gamma 函数,我们可以把 $f(x)$ 表达为

还记得神奇的 Gamma 函数可以把很多数学概念从整数集合延拓到实数集合吧。我们在上式中取$\alpha=k, \beta=n-k+1$, 于是我们得到
\begin{equation}
f(x) = \frac{\Gamma(\alpha+\beta)}{\Gamma(\alpha)\Gamma(\beta)}x^{\alpha-1}(1-x)^{\beta-1}
\end{equation}
这个就是一般意义上的 Beta 分布!可以证明,在$\alpha,\beta$取非负实数的时候,这个概率密度函数也都是良定义的。
好,我们回到魔鬼的游戏,这$n=10,k=7$这个具体的实例中,我们按照如下密度分布的峰值去猜测才是最有把握的。
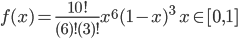
然而即便如此,我们能做到一次猜中的概率也不高,很不幸,你第一次没有猜中,魔鬼微笑着说:“我再仁慈一点,再给你一个机会,你按5下这个机器,你就得到了5个[0,1]之间的随机数,然后我可以告诉你这5个数中的每一个,和我的第7大的数相比,谁大谁小,然后你继续猜我手头的第7大的数是多少。”这时候我们应该怎么猜测呢?

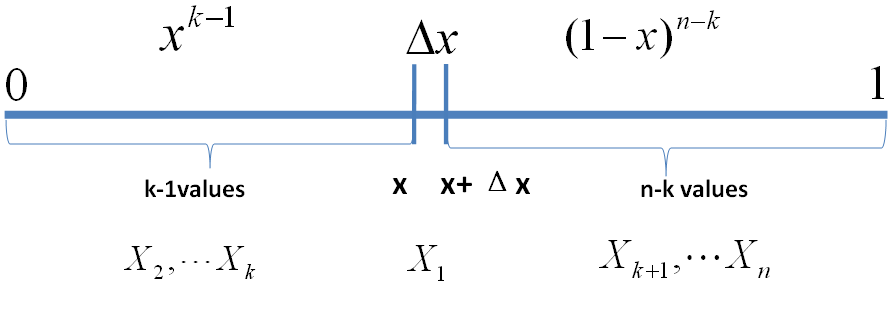
老师,我对最后的那句【我们按照如下密度分布的峰值去猜测才是最有把握的】有两个问题:1.概率密度的峰值我实在不懂,从网上找了很多也没看懂,希望你能给我讲解一下。2.f(x)的函数形式有了,能不能以魔鬼的问题为例,再说一下怎么猜测呢?谢谢了。
[回复]
massz 回复:
24 1 月, 2013 at 08:26
我理解最后的结论f(x)就是X7的在0到1上的分布概率,所以应该猜 n=argmax f(x)。
这是我个人的理解。如果不正确还请指教。
我的概率基础很弱,但是这篇讲义非常赞。几乎只要读者了解概率基础就可以理解这篇文章。让我对beta分布有了全新的认识。非常感谢作者。
[回复]
ppmmlong 回复:
26 1 月, 2013 at 12:51
嗯,嗯,作者能这么无私的讲解真是非常令人感谢。你的理解也让我明白了,谢谢了。
[回复]
king 回复:
9 6 月, 2013 at 16:50
这是密度函数求点区间的极值就是此点的概率问题。
[回复]
川 回复:
16 5 月, 2015 at 15:02
我感觉这个问题上,作者出了些错误。求得是第七大的数,将其分布在(0,1)上,也就是说(0,x)之间有三个,(x,1)之间有六个。那么这个式子应该是[10!/(3!*6!)]*x^3*(1-x)6
[回复]
老师,请教一下。我对最后的那句【我们按照如下密度分布的峰值去猜测才是最有把握的】有两个问题:1.概率密度的峰值我实在不懂,从网上找了很多也没看懂,希望你能给我讲解一下。2.f(x)的函数形式有了,能不能以魔鬼的问题为例,再说一下怎么猜测呢?谢谢了。
[回复]
我想问一下,你这些资料是参考了什么课本的呢?我想系统地学习一下。
[回复]
rickjin 回复:
25 3 月, 2013 at 18:19
就是 wikipeida 和网络上零碎的资料, 主要靠自己思考, 没有什么课本可以参考
[回复]
lijing 回复:
28 3 月, 2013 at 22:51
我看了Bishop的PRML中的2.1.1之后,总是不明白为什么可以使用Beta分布来作为u的先验分布,u不一定就服从这个Beta分布啊,怎么能够就直接用了,总觉得是不是我哪里理解错了呢?不知道你是怎么理解的呢?
[回复]
n,k=10,7
=>
α,ß=7,4
f(x)怎么出现(6)!和(3)!?是不是笔误啊?
[回复]
whille 回复:
1 5 月, 2013 at 13:50
明白了,没问题
[回复]
whille 回复:
2 5 月, 2013 at 10:01
x in [0,1], 7th is 4. α,ß=4,7才对吧,结果这里beta分布的最大概率在0.3左右。 另外beta分布的pdf为什么没有归一化呢? f(x)最大值>2.5了。
[回复]
P(E)=∏i=1nP(Xi) 这个式子不对吧,应该在前面加上[(k-1)!]*[(n-k)!]/n!这个吧!
[回复]
您好,这里的第7大是不是有歧义?按照文章的描述,感觉应该是第7小啊,从0至1的过程中,数到7,不应该是第7小的吗?谢谢!
[回复]