LDA-math-神奇的Gamma函数(3)

1. 神奇的Gamma函数
1.3 从二项分布到Gamma 分布

Gamma 函数在概率统计中频繁现身，众多的统计分布，包括常见的统计学三大分布($t$ 分布，$\chi^2$ 分布，$F$ 分布)、Beta分布、 Dirichlet 分布的密度公式中都有 Gamma 函数的身影；当然发生最直接联系的概率分布是直接由 Gamma 函数变换得到的 Gamma 分布。对Gamma 函数的定义做一个变形，就可以得到如下式子

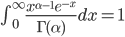
于是，取积分中的函数作为概率密度，就得到一个形式最简单的Gamma 分布的密度函数

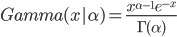
如果做一个变换 $x=\beta t$, 就得到Gamma 分布的更一般的形式

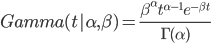
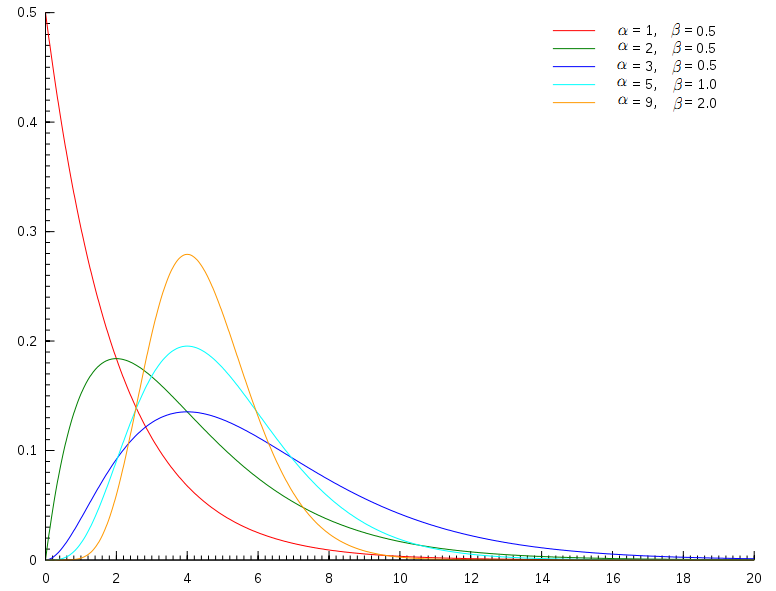
其中 $\alpha$ 称为 shape parameter, 主要决定了分布曲线的形状;而$\beta$ 称为 rate parameter 或者inverse scale parameter ($\frac{1}{\beta}$ 称为scale parameter),主要决定曲线有多陡。

$Gamma(t|\alpha,\beta)$分布图像

Gamma 分布在概率统计领域也是一个万人迷，众多统计分布和它有密切关系。指数分布和$\chi^2$ 分布都是特殊的Gamma 分布。另外Gamma 分布作为先验分布是很强大的，在贝叶斯统计分析中被广泛的用作其它分布的先验。如果把统计分布中的共轭关系类比为人类生活中的情侣关系的话，那指数分布、Poission分布、正态分布、对数正态分布都可以是 Gamma 分布的情人。接下来的内容中中我们主要关注$\beta = 1$的简单形式的 Gamma 分布。

Gamma 分布首先和 Poisson 分布、Poisson 过程发生密切的联系。我们容易发现Gamma 分布的概率密度和 Poisson 分布在数学形式上具有高度的一致性。参数为$\lambda$的Poisson 分布，概率写为

在 Gamma 分布的密度中取 $\alpha = k+1$ 得到

所以这两个分布数学形式上是一致的，只是 Poisson 分布是离散的，Gamma 分布是连续的，可以直观的认为 Gamma 分布是 Poisson 分布在正实数集上的连续化版本。

这种数学上的一致性是偶然的吗？这个问题我个人曾经思考了很久，终于想明白了从二项分布出发能把 Gamma 分布和 Poisson 分布紧密联系起来。我们在概率统计中都学过 $Poisson(\lambda)$ 分布可以看成是二项分布 $B(n,p)$ 在 $np=\lambda, n \rightarrow \infty$ 条件下的极限分布。如果你对二项分布关注的足够多，可能会知道二项分布的随机变量$X\sim B(n,p)$满足如下一个很奇妙的恒等式
\begin{equation}
\label{binomial-beta}
P(X \le k) = \frac{n!}{k!(n-k-1)!} \int_p^1 t^k(1-t)^{n-k-1} dt  \quad  (*)
\end{equation}

这个等式反应的是二项分布和 Beta 分布之间的关系，证明并不难，它可以用一个物理模型直观的做概率解释，而不需要使用复杂的数学分析的方法做证明。由于这个解释和 Beta 分布有紧密的联系，所以这个直观的概率解释我们放到下一个章节，讲解 Beta/Dirichlet 分布的时候进行。此处我们暂时先承认(*)这个等式成立。我们在等式右侧做一个变换$t=\frac{x}{n}$,得到
\begin{align}
P(X \le k) & = \frac{n!}{k!(n-k-1)!} \int_p^1 t^k(1-t)^{n-k-1} dt \notag \\
& = \frac{n!}{k!(n-k-1)!} \int_{np}^{n} (\frac{x}{n})^k(1-\frac{x}{n})^{n-k-1} d\frac{x}{n} \notag \\
& = \frac{(n-1)!}{k!(n-k-1)!} \int_{np}^{n} (\frac{x}{n})^k(1-\frac{x}{n})^{n-k-1} dx \notag \\
& = \int_{np}^{n} \binom{n-1}{k}(\frac{x}{n})^k(1-\frac{x}{n})^{n-k-1} dx \notag \\
& = \int_{np}^{n} Binomial(Y=k|n-1,\frac{x}{n})dx
\end{align}
上式左侧是二项分布 $B(n,p)$, 而右侧为无穷多个二项分布 $B(n-1,\frac{x}{n})$的积分和, 所以可以写为
\begin{equation}
\label{binomial-beta-binomial}
Binomial(X \le k|n,p) = \int_{np}^{n} Binomial(Y=k|n-1,\frac{x}{n})dx  \quad
\end{equation}
实际上，对上式两边在条件$np=\lambda, n \rightarrow \infty$ 下取极限，则左边有 $B(n,p) \rightarrow Poisson(\lambda)$, 而右边有$B(n-1,\frac{x}{n}) \rightarrow Poisson(x)$,所以得到
\begin{equation}
Poisson(X \le k|\lambda) = \int_\lambda^\infty Poisson(Y=k|x)dx
\end{equation}
把上式右边的Possion 分布展开，于是得到

所以对于们得到如下一个重要而有趣的等式
\begin{equation}
\label{poisson-gamma}
Poisson(X \le k|\lambda) = \int_\lambda^\infty \frac{x^k e^{-x}}{k!} dx  \quad   (**)
\end{equation}

接下来我们继续玩点好玩的，对上边的等式两边在 $\lambda \rightarrow 0$ 下取极限，左侧Poisson分布是要至少发生k个事件的概率， $\lambda \rightarrow 0$ 的时候就不可能有事件发生了，所以 $P(X \le k)\rightarrow 1$, 于是我们得到

在这个积分式子说明 $f(x) = \frac{x^k e^{-x}}{k!} $在正实数集上是一个概率分布函数，而这个函数恰好就是Gamma 分布。我们继续把上式右边中的 $k!$ 移到左边，于是得到

于是我们得到了 $k!$ 表示为积分的方法。

看，我们从二项分布的一个等式出发, 同时利用二项分布的极限是Possion 分布这个性质，基于比较简单的逻辑，推导出了 Gamma 分布，同时把 $k!$ 表达为 Gamma 函数了！实际上以上推导过程是给出了另外一种相对简单的发现 Gamma 函数的途径。

回过头我们看看(**)式,非常有意思，它反应了Possion 分布和 Gamma 分布的关系，这个和(*)式中中反应的二项分布和Beta 分布的关系具有完全相同的结构。把(**)式变形一下得到

我们可以看到，Poisson分布的概率累积函数和Gamma 分布的概率累积函数有互补的关系。

其实(*)和(**)这两个式子都是陈希儒院士的《概率论与数理统计》这本书第二章的课后习题，不过陈老师习题答案中给的证明思路是纯粹数学分析的证明方法，虽然能证明等式成立，但是看完证明后无法明白这两个等式是如何被发现的。上诉的论述过程说明，从二项分布出发，这两个等式都有可以很好的从概率角度进行理解。希望以上的推导过程能给大家带来一些对 Gamma 函数和 Gamma 分布的新的理解，让Gamma 分布不再神秘。