
四、众里寻她千百度,误差分布曲线的确立
第三个故事有点长,主角是高斯和拉普拉斯,故事的主要内容是猜测上帝的造物的旨意,寻找随机误差分布的规律。
天文学是第一个被测量误差困扰的学科,从古代至十八世纪天文学一直是应用数学最发达的领域, 到十八世纪,天文学的发展积累了大量的天文学数据需要分析计算,应该如何来处理数据中的观测误差成为一个很棘手的问题。 我们在数据处理中经常使用平均的常识性法则,千百来来的数据使用经验说明算术平均能够消除误差,提高精度。 平均有如此的魅力,道理何在,之前没有人做过理论上的证明。 算术平均的合理性问题在天文学的数据分析工作中被提出来讨论:测量中的随机误差服应该服从怎样的概率分布? 算术平均的优良性和误差的分布有怎样的密切联系?
伽利略在他著名的《关于两个主要世界系统的对话》中,对误差的分布做过一些定性的描述,主要包括:
- 误差是对称分布的;
- 大的误差出现频率低,小的误差出现频率高。
用数学的语言描述,也就是说误差分布函数 $f(x)$ 关于0对称分布,概率密度随 $|x|$ 增加而减小, 这两个定性的描述都很符合常识。
许多天文学家和数学家开始了寻找误差分布曲线的尝试。 Thomas Simpson (1710-1761) 先走出了有意义的一步。 设真值为 $\theta$, $x_1, \cdots, x_n$为n次测量值, 每次测量的误差为$ e_i = x_i - \theta $, 若用算术平均 $\bar{x} = \frac{\sum_{i=1}^n x_i}{n} $去估计$\theta$, 其误差为 $\bar{e} = \frac{\sum_{i=1}^n e_i}{n} $。 Simpson 证明了, 对于如下的一个概率分布,
【Simpson 的误差态分布曲线】
有
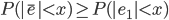
也就是说,$|\bar{e}|$ 相比于$|e_1|$取小值的机会更大。 Simpson 的这个工作很粗糙,但是这是第一次在一个特定情况下,从概率论的角度严格证明了算术平均的优良性。
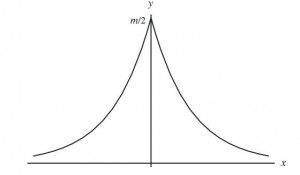
从 1772-1774 年, 拉普拉斯也加入到了寻找误差分布函数的队伍中。拉普拉斯假定误差分布函数$f(x)$满足如下性质
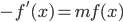
由此最终求得的分布函数为
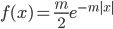
这个函数现在被称为拉普拉斯分布。
【Laplace 的误差态分布曲线】
以这个函数作为误差分布,拉普拉斯开始考虑如何基于测量的结果去估计未知参数的值。 拉普拉斯可以算是一个贝叶斯主义者,他的参数估计的原则和现代贝叶斯方法非常相似,假设先验分布是均匀的, 计算出参数的后验分布后,取后验分布的中值点,即$1/2$分位点,作为参数估计值。可是基于这个误差分布函数 做了一些计算之后,拉普拉斯发现计算过于复杂,最终没能给出什么有用的结果。
拉普拉斯可是概率论的大牛,写过两本极有影响力的《概率分析理论》, 不过以我的数学审美,实在无法理解拉普拉斯这样的大牛怎么找了一个零点不可导的误差的分布函数, 拉普拉斯最终还是没能搞定误差分布的问题。
现在轮到高斯登场了,高斯在数学史中的地位极高,号称数学史上的狐狸,数学家阿贝尔对他的评论是 "He is like the fox, who effaces his tracks in the sand with his tail." 我们的数学大师陈省身把黎曼和庞加莱称为数学家中的菩萨,而称自己为罗汉;高斯是黎曼的导师,数学圈里有些教授把高斯称为数学家中的佛。 在数学家中既能仰望理论数学的星空,又能脚踏应用数学的实地的可不多见, 高斯是数学家中少有的顶”天“立”地“的人物,他既对纯理论数学有深刻的洞察力,又极其重视数学在实践中的应用。 在误差分布的处理中,高斯以及其简单的手法确立了随机误差的概率分布,其结果成为数理统计发展史上的一块里程碑。
高斯的介入首先要从天文学界的一个事件说起。1801年1月,天文学家Giuseppe Piazzi发现了一颗从未见过 的光度8等的星在移动, 这颗现在被称作谷神星(Ceres)的小行星在夜空中出现6个星期,扫过八度角后在就在太阳的光芒下没了踪影,无法观测。 而留下的观测数据有限,难以计算出他的轨道,天文学家也因此无法确定这颗新星是彗星还是行星, 这个问题很快成了学术界关注的焦点。高斯当时已经是很有名望的年轻数学家了, 这个问题引起了他的兴趣。高斯以其卓越的数学才能创立了一种崭新的 行星轨道的计算方法,一个小时之内就计算出了行星的轨道,并预言了他在夜空中出现的时间和位置。 1801年12月31日夜,德国天文爱好者奥伯斯(Heinrich Olbers),在高斯预言的时间里,用望远镜对准了这片天空。 果然不出所料,谷神星出现了!
高斯为此名声大震,但是高斯当时拒绝透露计算轨道的方法,原因可能是高斯认为自己的方法的理论基础还不够成熟, 而高斯一向治学严谨、精益求精,不轻易发表没有思考成熟的理论。直到1809年高斯系统地完善了相关的数学理论后, 才将他的方法公布于众,而其中使用的数据分析方法,就是以正态误差分布为基础的最小二乘法。 那高斯是如何推导出误差分布为正态分布的?让我们看看高斯是如何猜测上帝的意图的。
设真值为 $\theta$, $x_1, \cdots, x_n$为n次独立测量值, 每次测量的误差为$ e_i = x_i - \theta $, 假设误差$e_i$的密度函数为 f(e), 则测量值的联合概率为n个误差的联合概率,记为
\begin{equation}
L(\theta) = L(\theta;x_1,\cdots,x_n)=f(e_1)\cdots f(e_n) = f(x_1-\theta)\cdots f(x_n-\theta)
\end{equation}
但是高斯不采用贝叶斯的推理方式,而是直接取$L(\theta)$达到最大值的 $\hat{\theta}=\hat{\theta}(x_1,\cdots,x_n)$ 作为$\theta$的估计值,即

现在我们把$L(\theta)$ 称为样本的似然函数,而得到的估计值$ \hat{\theta}$ 称为极大似然估计。 高斯首次给出了极大似然的思想,这个思想后来被统计学家 R.A.Fisher 系统的发展成为参数估计中的极大似然估计理论。
高斯接下来的想法特别牛,他开始揣度上帝的意图,而这充分体现了高斯的数学天才。 高斯把整个问题的思考模式倒过来:既然千百年来大家都认为算术平均 是一个好的估计,那我就认为极大似然估计导出的就应该是算术平均!所以高斯猜测上帝在创世纪中的旨意就是:
误差分布导出的极大似然估计 = 算术平均值
然后高斯去找误差密度函数 $f$ 以迎合这一点。即寻找这样的概率分布函数 $f$, 使 得极大似然估计正好是算术平均 $\hat{\theta} = \bar{x}$。而高斯应用数学技巧求解这个函数$f$, 高斯证明(证明不难,后续给出),所有的概率密度函数中,唯一满足这个性质的就是
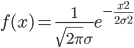
瞧,正态分布的密度函数 $N(0, \sigma^2)$ 被高斯他老人家给解出来了!
【正态误差态分布律】
进一步,高斯基于这个误差分布函数对最小二乘法给出了一个很漂亮的解释。 对于每个误差 $e_i$,有 $e_i \sim N(0, \sigma^2)$, 则$(e_1, \cdots, e_n)$ 的联合概率分布为
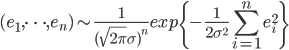
要使得这个概率最大,必须使得$\sum_{i=1}^n e_i^2 $ 取最小值,这正好就是最小二乘法的要求。
高斯所拓展的最小二乘法成为了十九世纪统计学的最重要成就,它在十九世纪统计学的重要性就相当于十八世紀的微积分之于数学。 而勒让德和最小二乘的的发明权之争,成了数学史上仅次于牛顿、莱布尼茨微积分发明的争端。 相比于勒让德1805给出的最小二乘法描述,高斯基于误差正态分布的最小二乘理论显然更高一筹, 高斯的工作中既提出了极大似然估计的思想,又解决了误差的概率密度分布的问题, 由此我们可以对误差的大小的影响进行统计度量了。高斯的这项工作对后世的影响极大,而正态分布也因此被冠名 高斯分布。估计高斯本人当时是完全没有意识到他的这个工作给现代数理统计学带来的深刻影响。 高斯在数学上的贡献特多,去世前他是要求给自己的墓碑上雕刻上正十七边形,以说明他在正十七边形尺规作图上的杰出工作。 而后世的德国钞票和钢镚上是以正态密度曲线来纪念高斯,这足以说明高斯的这项工作在当代科学发展中的份量。
17-18世纪科学界流行的做法,是尽可能从某种简单明了的准则(first principle)出发进行推导, 高斯设定的准则“最大似然估计应该导出优良的算术平均”,并导出了误差服从正态分布,推导的形式上非常简洁优美。 但是高斯给的准则在逻辑上并不足以让人完全信服,因为算术平均的优良性当时更多的是一个直觉经验,缺乏严格的理论支持。 高斯的推导存在循环论证的味道:因为算术平均是优良的,推出误差必须服从正态分布; 反过来,又基于正态分布推导出最小二乘和算术平均,来说明最小二乘法和算术平均的优良性。 这陷入了一个鸡生蛋蛋生鸡的怪圈,逻辑上算术平均的优良性到底有没有自行成立的理由呢?
高斯的文章发表之后,拉普拉斯很快得知了高斯的工作。 拉普拉斯看到,正态分布既可以从作为抛钢镚产生的序列和中生成出来,又可以被优雅的作为误差分布定律, 这难道是偶然现象?拉普拉斯不愧为概率论的大牛,他马上将误差的正态分布理论和中心极限定理联系起来,提出了元误差解释。 他指出如果误差可以看成许多量的叠加,则根据他的中心极限定理,则随机误差理所应当是高斯分布。 而20世纪中心极限定理的进一步发展,也给这个解释提供了更多的理论支持。因此有了这个解释为出发点, 高斯的循环论证的圈子就可以打破。 估计拉普拉斯悟出这个结论之后一定想撞墙,自己辛辛苦苦寻寻觅觅 了这么久的误差分布曲线就在自己的眼皮底下,自己却长年来视而不见,被高斯给占了先机。
至此,误差分布曲线的寻找尘埃落定,正态分布在误差分析中确立了自己的地位,开始并在整个19世纪不断的开疆扩土, 直至在统计学中鹤立鸡群,傲世其它一切概率分布;而高斯和拉普拉斯的工作,为现代统计学的发展开启了一扇大门。
在整个正态分布被发现与应用的历史中,棣莫弗、拉普拉斯、高斯各有贡献,拉普拉斯从中心极限定理的角度解释它, 高斯把它应用在误差分析中,殊途同归。正态分布被人们发现有这么好的性质,各国人民都争抢他的冠名权。 因为 Laplace 是法国人,所以当时在法国被称为拉普拉斯分布; 而高斯是德国人, 所以在德国叫做高斯分布;第三中立国的人民称他为拉普拉斯-高斯分布。后来法国的大数学家庞加莱(Henri Poincaré)建议改用正态分布这一中立名称,而随后统计学家卡尔.皮尔森使得这个名称被广泛接受:
Many years ago I called the Laplace-Gaussian curve the normal curve, which name, while it avoids an international question of priority, has the disadvantage of leading people to believe that all other distributions of frequency are in one sense or another "abnormal".}
-Karl Pearson (1920)
不过因为高斯在数学家中的名气是在太大, 正态分布的桂冠还是更多的被戴在了高斯的脑门上,目前数学界通行的用语是正态分布高斯分布, 两者并用。
正态分布在高斯的推动下,迅速在测量误差分析中被广泛使用,然而早期也仅限于测量误差的分析中, 其重要性远没有被自然科学和社会科学领域中的学者们所认识,那正态分布是如何从测量误差分析的小溪, 冲向自然科学和社会科学的汪洋大海的呢?

还有吧,想继续看!
[回复]
rickjin 回复:
12 10 月, 2012 at 22:30
还有3个章节,不过接下来的这个章节写得慢,要过两天才能贴出来
[回复]
讲的很好啊,但是公式排版还是不好看啊,都乱了呢
[回复]
rickjin 回复:
27 10 月, 2012 at 01:05
你那网络有问题?我这看排版是很整齐的
[回复]
"简单明了的准则"是否应译作Occam's Razor?
[回复]
哇哈哈,,看的热血澎湃,谢谢作者,太给力了,,高斯太屌了,拉普拉斯感觉也很吊
[回复]
写的真好啊,总结一下:拉普拉斯通过二项分布的极限分部推导出正态分布的概率密度函数,高斯则通过假设误差分布的极大似然估计为算术平均数反向推导出正态分布的概率密度函数,并循环证明了最小二乘法优良的性质。
[回复]