正态分布的前世今生(二)

三、最小二乘法，数据分析的瑞士军刀

第二个故事的主角是欧拉(Euler), 拉普拉斯(Lapalace),勒让德Legendre) 和高斯(Gauss),故事发生的时间是十八世纪中到十九世纪初。十七、十八世纪是科学发展的黄金年代，微积分的发展和牛顿万有引力定律的建立，直接的推动了天文学和测地学的迅猛发展。当时的大科学家们都在考虑许多天文学上的问题。几个典型的问题如下：

• 土星和木星是太阳系中的大行星，由于相互吸引对各自的运动轨道产生了影响，许多大数学家，包括欧拉和拉普拉斯都在基于长期积累的天文观测数据计算土星和木星的运行轨道。
• 勒让德承担了一个政府给的重要任务，测量通过巴黎的子午线的长度，
• 海上航行经纬度的定位。主要是通过对恒星和月面上的一些定点的观测来确定经纬度。

这些天文学和测地学的问题，无不涉及到数据的多次测量，数据的计算与分析；十七、十八世纪的天文观测，也积累了大量的数据需要进行分析和计算。很多年以前，学者们就已经经验性的认为，对于有误差的测量数据，多次测量取平均是比较好的处理方法，虽然缺乏理论上的论证，也不断的受到一些人的质疑。取平均作为一种异常直观的方式，已经被使用了千百年,在多年积累的数据的处理经验中也得到一定的验证，被认为是一种良好的数据处理方法。

以上涉及的问题，我们直接关心的目标量往往无法直接观测，但是一些相关的量是可以观测到的，而通过建立数学模型，最终可以解出我们关心的量。这些天文学的问题大体都可以转换为描述如下的问题：有我们想估计的量 $\beta_0,\cdots,\beta_p$, 另有若干个可以测量的量 $x_1,\cdots,x_p, y$, 这些量之间有线性关系

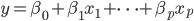
如何通过多组观测数据求解出参数$\beta_0,\cdots,\beta_p$呢？ 欧拉和拉普拉斯采用的都是求解线性方程组的方法。

\begin{eqnarray}
\left\{
\begin{array}{lll}
y_1 = \beta_0 + \beta_1x_{11} + \cdots + \beta_px_{p1} \\
y_2 = \beta_0 + \beta_1x_{12} + \cdots + \beta_px_{p2} \\
\vdots \\
y_n = \beta_0 + \beta_1x_{1n} + \cdots + \beta_px_{pn}
\end{array}
\right.
\end{eqnarray}

但是面临的一个问题是，有 $n$ 组观测数据，$p + 1$ 个变量， 如果 $n > p + 1$, 则得到的线性矛盾方程组，无法直接求解。 所以欧拉和拉普拉斯采用的方法都是通过一定的对数据的观察，把$n$个线性方程分为 $p+1$组，然后把每个组内的方程线性求和后归并为一个方程，从而就把$n$个方程的方程组划归为$p+1$个方程的方程组，进一步解方程求解参数。这些方法初看有一些道理，但是都过于 adhoc, 无法形成统一处理这一类问题的一个通用解决框架。

以上求解线性矛盾方程的问题在现在的本科生看来都不困难，就是统计学中的线性回归问题，直接用最小二乘法就解决了，可是即便如欧拉、拉普拉斯这些数学大牛，当时也未能对这些问题提出有效的解决方案。可见在科学研究中，要想在观念上有所突破并不容易。有效的最小二乘法是勒让德在 1805 年发表的，基本思想就是认为测量中有误差，所以所有方程的累积误差为

累积误差 = $\sum($ 观测值 - 理论值 $)^2$

我们求解出导致累积误差最小的参数即可。

\begin{eqnarray}
\label{least-square-error}
\begin{array}{lll}
\hat{\beta}& = & \displaystyle argmin_{\beta} \sum_{i=1}^n e_i^2 \\
& = & \displaystyle
argmin_{\beta} \sum_{i=1}^n [y_i - (\beta_0 + \beta_1x_{1i} + \cdots + \beta_px_{pi})]^2
\end{array}
\end{eqnarray}

勒让德在论文中对最小二乘法的优良性做了几点说明：

•  最小二乘使得误差平方和最小，并在各个方程的误差之间建立了一种平衡，从而防止某一个极端误差取得支配地位
•  计算中只要求偏导后求解线性方程组，计算过程明确便捷
• 最小二乘可以导出算术平均值作为估计值

对于最后一点，从统计学的角度来看是很重要的一个性质。推理如下：假设真值为 $\theta$, $x_1, \cdots, x_n$为n次测量值, 每次测量的误差为$ e_i = x_i - \theta $，按最小二乘法，误差累积为

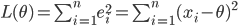
求解$\theta$ 使得 $L(\theta)$达到最小，正好是算术平均 $\bar{x} = \frac{\sum_{i=1}^n x_i}{n} $。

由于算术平均是一个历经考验的方法，而以上的推理说明，算术平均是最小二乘的一个特例，所以从另一个角度说明了最小二乘方法的优良性，使我们对最小二乘法更加有信心。

最小二乘法发表之后很快得到了大家的认可接受，并迅速的在数据分析实践中被广泛使用。不过历史上又有人把最小二乘法的发明归功于高斯，这又是怎么一回事呢。高斯在1809年也发表了最小二乘法，并且声称自己已经使用这个方法多年。高斯发明了小行星定位的数学方法，并在数据分析中使用最小二乘方法进行计算，准确的预测了谷神星的位置。

扯了半天最小二乘法，没看出和正态分布有任何关系啊，离题了吧？单就最小二乘法本身，虽然很实用，不过看上去更多的算是一个代数方法，虽然可以推导出最优解，对于解的误差有多大，无法给出有效的分析，而这个就是正态分布粉墨登场发挥作用的地方。勒让德提出的最小二乘法，确实是一把在数据分析领域披荆斩棘的好刀，但是刀刃还是不够锋利；而这把刀的打造后来至少一半功劳被归到高斯，是因为高斯不单独自的给出了造刀的方法，而且把最小二乘这把利刀的刀刃造得无比锋利，把最小二乘打造为了一把瑞士军刀。高斯拓展了最小二乘法，把正态分布和最小二乘法联系在一起，并使得正态分布在统计误差分析中确立了自己的定位，否则正态分布就不会被称为高斯分布了。 那高斯这位神人是如何把正态分布引入到误差分析之中，打造最小二乘这把瑞士军刀的呢？看下一个故事。