正态分布的前世今生(四)

(五)曲径通幽处，禅房花木深，正态分布的各种推导

在介绍正态分布的后续发展之前，我们来多讲一点数学，也许有些人会觉得枯燥，不过高斯曾经说过：“数学是上帝的语言”。所以要想更加深入的理解正态分布的美，唯有通过上帝的语言。

造物主造物的准则往往是简单明了的，只是在纷繁芜杂的万物之中，我们要发现并领会它并非易事。之前提到过，17-18世纪科学界流行的做法，是尽可能从某种简单明了的准则(first principle)出发作为我们探求的起点，而后来的数学家和物理学家们研究发现，屡次从一些给定的简单的准则出发,我们总是被引领到了正态分布的家门口，这让人感觉到正态分布的美妙。

达尔文的表弟高尔顿是生物学家兼统计学家，他对正态分布非常的推崇与赞美：”我几乎不曾见过像误差呈正态分布这么激发人们无穷想象的宇宙秩序“。当代两位伟大的概率学家 Levy 和 Kac 都曾经说过， 正态分布是他们切入概率论的初恋情人，具有无穷的魅力。如果古希腊人知道正态分布，想必奥林匹斯山的神殿里会多出一个正态女神，由她来掌管世间的混沌。

要拉下正态分布的神秘面纱展现她的美丽，需要高深的概率论知识，本人在数学方面知识浅薄，不能胜任。只能在极为有限的范围内尝试掀开她的面纱的一角。棣莫弗和拉普拉斯以抛钢镚的序列求和为出发点，沿着一条小径把我们第一次领到了正态分布的家门口，这条路叫作中心极限定理，而这条路上风景秀丽，许多概率学家都为之倾倒，这条路在20世纪被概率学家们越拓越宽。而后数学家和物理学家们发现：条条曲径通正态。著名的物理学家 E.T.Jaynes 在他的名著《Probability Theory, the Logic of Science》(中文书名翻译为《概率论沉思录》)中，描绘了四条通往正态分布的小径。曲径通幽处，禅房花木深，让我们一起来欣赏一下四条小径上的风景吧。

1. 高斯的推导(1809)

第一条小径是高斯找到的，高斯以如下准则作为小径的出发点

误差分布导出的极大似然估计 = 算术平均值

设真值为 $\theta$, $x_1, \cdots, x_n$为n次独立测量值, 每次测量的误差为$ e_i = x_i - \theta $，

假设误差$e_i$的密度函数为 f(e), 则测量值的联合概率为n个误差的联合概率，记为

\begin{equation}
L(\theta) = L(\theta;x_1,\cdots,x_n)=f(e_1)\cdots f(e_n) = f(x_1-\theta)\cdots f(x_n-\theta)
\end{equation}

为求极大似然估计，令

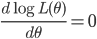
整理后可以得到

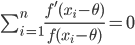
令 $g(x) = \frac{f'(x)}{f(x)}$,

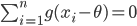
由于高斯假设极大似然估计的解就是算术平均 $\bar{x}$，把解带入上式，可以得到

\begin{equation}
\label{gauss-derivation}
\sum_{i=1}^n g(x_i-\bar{x}) = 0     (*)
\end{equation}

(*) 式中取 $n=2$, 有

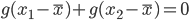
由于此时有 $ x_1-\bar{x} = -(x_2-\bar{x})$, 并且 $x_1, x_2$ 是任意的，有此得到

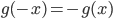
(*) 式中再取 $n=m+1$, 并且要求 $x_1=\cdots=x_m=-x, x_{m+1} = mx$, 则有 $\bar{x} = 0$, 并且

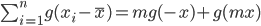
所以得到

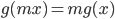
而满足上式的唯一的连续函数就是 $g(x)=cx$, 从而进一步可以求解出

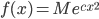
由于$f(x)$是概率分布函数，把$f(x)$ 正规化一下就得到正态分布函数。

2. Herschel(1850)和 Maxwell(1860) 的推导

第二条小径是天文学家 Hershcel 和物理学家麦克斯韦(Maxwell) 发现的。1850年，天文学家 John Herschel 在对星星的位置进行测量的时候，需要考虑二维的误差分布，为了推导这个误差的概率密度分布 $f(x,y)$,Herschel 设置了两个准则：

•  x 轴和 y 轴的误差是相互独立的，即误差的概率在正交的方向上相互独立
• 误差的概率分布在空间上具有旋转对称性，即误差的概率分布和角度没有关系

这两个准则对于 Herschel 考虑的实际测量问题看起来都很合理。由准则1，可以得到 $f(x,y)$ 应该具有如下形式

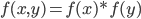
把这个函数转换为极坐标，在极坐标下的概率密度函数设为 $g(r,\theta)$, 有

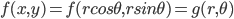
由准则2, $g(r,\theta)$ 具有旋转对称性，也就是应该和 $\theta$ 无关, 所以 $g(r,\theta)=g(r)$,
综合以上，我们可以得到

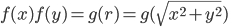
取 $y=0$, 得到 $g(x) = f(x)f(0)$, 所以上式变为

令 $\log[\frac{f(x)}{f(0)}] = h(x) $, 则有

从这个函数方程中容易求解出 $h(x) = ax^2$, 从而可以得到 $f(x)$ 的一般形式如下

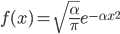
而 $f(x)$ 就是正态分布 $N(0, 1/\sqrt{2\alpha)}$， 而 $f(x,y)$ 就是标准二维正态分布函数。

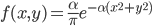
1860 年，我们伟大的物理学家麦克斯韦在考虑气体分子的运动速度分布的时候，在三维空间中基于类似的准则推导出了气体分子运动的分布是正态分布$\rho(v_x,v_y,v_z) \propto exp\{-\alpha(v_x^2+v_y^2+v_z^2)\} $。这就是著名的麦克斯韦分子速率分布定律。大家还记得我们在普通物理中学过的麦克斯韦-波尔兹曼气体速率分布定律吗？

\begin{eqnarray}
\label{maxwell}
\begin{array}{lll}
F(v) & = & \displaystyle (\frac{m}{2\pi kT})^{3/2} e^{-\frac{mv^2}{2kT}} \\
& = & \displaystyle (\frac{m}{2\pi kT})^{1/2} e^{-\frac{mv_x^2}{2kT}} \times (\frac{m}{2\pi kT})^{1/2} e^{-\frac{mv_y^2}{2kT}} \times (\frac{m}{2\pi kT})^{1/2} e^{-\frac{mv_z^2}{2kT}}
\end{array}
\end{eqnarray}

所以这个分布其实是三个正态分布的乘积,你的物理老师是否告诉过你其实这个分布就是三维正态分布？反正我是一直不知道，直到今年才明白 🙂

Herschel-Maxwell 推导的神妙之处在于，没有利用任何概率论的知识，只是基于空间几何的不变性，就推导出了正态分布。

3. Landon 的推导(1941)

第三条道是一位电气工程师，Vernon D. Landon 给出的。1941 年，Landon 研究通信电路中的噪声电压，通过分析经验数据他发现噪声电压的分布模式很相似，不同的是分布的层级，而这个层级可以使用方差 $\sigma^2$ 来刻画。因此他推理认为噪声电压的分布函数形式是 $p(x;\sigma^2)$。现在假设有一个相对于 $\sigma$而言很微小的误差扰动 $e$，$e$ 的分布函数是 $q(e)$, 那么新的噪声电压是 $x' = x + e$。Landon 提出了如下的准则

•  随机噪声具有稳定的分布模式
• 累加一个微小的随机噪声，不改变其稳定的分布模式，只改变分布的层级(用方差度量)

用数学的语言描述: 如果 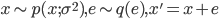则有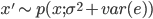

现在我们来推导满足以上两个准则的函数$p(x;\sigma^2)$ 应该长成啥样。按照两个随机变量和的分布的计算方式， $x'$ 的分布函数将是 $x$ 的分布函数和 $e$的分布函数的卷积，即有

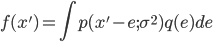
把 $p(x'-e; \sigma^2)$ 在$x'$处做泰勒级数展开(为了方便，展开后把自变量由 $x'$ 替换为 $x$)， 上式可以展开为

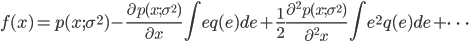
记 $p=p(x; \sigma^2)$,则有

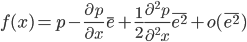
对于微小的随机扰动 $e$, 我们认为他取正值或者负值是对称的，所以$\bar{e} = 0 $。所以有

\begin{equation}
\label{landon-x}
f(x) = p + \frac{1}{2} \frac{\partial^2 p}{\partial^2 x}\bar{e^2} + o(\bar{e^2})
\end{equation}

对于新的噪声电压是 $x' = x + e$， 方差由$\sigma^2$ 增加为 $\sigma^2 + var(e) = \sigma^2 + \bar{e^2}$,所以按照 Landon 的分布函数模式不变的假设， 新的噪声电压的分布函数应该为 $f(x) = p(x; \sigma^2 + \bar{e^2})$ 。把$p(x; \sigma^2 + \bar{e^2})$ 在 $\sigma^2$ 处做泰勒级数展开，得到

\begin{equation}
\label{landon-sigma}
\displaystyle f(x) = p + \frac{\partial p}{\partial \sigma^2}\bar{e^2} + o(\bar{e^2})
\end{equation}

比较 以上 $f(x)$ 的两个展开式，可以得到如下偏微分方程

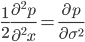
而这个方程就是物理上著名的扩散方程(diffusion equation),求解该方程就得到

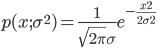
又一次，我们推导出了正态分布！

E.T. Jaynes对于这个推导的评价很高，认为Landon 的推导本质上给出了自然界的噪音形成的过程。他指出这个推导这基本上就是中心极限定理的增量式版本，相比于中心极限定理是一次性累加所有的因素，Landon 的推导是每次在原有的分布上去累加一个微小的扰动。
而在这个推导中，我们看到，正态分布具有相当好的稳定性；只要数据中正态的模式已经形成，他就容易继续保持正态分布，无论外部累加的随机噪声 $q(e)$ 是什么分布，正态分布就像一个黑洞一样把这个累加噪声吃掉。

4. 最大熵和正态分布

还有一条神妙的小径是基于最大熵原理的， 物理学家 E.T.Jaynes 在最大熵原理上有非常重要的贡献，他在《概率论沉思录》里面对这个方法有描述和证明，没有提到发现者，我不确认这条道的发现者是否是 E.T.Jaynes 本人。

熵在物理学中由来已久，信息论的创始人香农(Claude Elwood Shannon)把这个概念引入了信息论，学习机器学习的同学们都知道目前机器学习中有一个非常好用的分类算法叫最大熵分类器。要想把熵和最大熵的来龙去脉说清楚可不容易，希望我后续能有时间整理一下。这条道的风景是相当独特的，E.T.Jaynes 对这条道也是偏爱有加。

对于一个概率分布 $p(x)$, 我们定义他的熵为

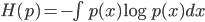
如果给定一个分布函数 $p(x)$ 的均值 $\mu$ 和方差$\sigma^2$(给定均值和方差这个条件，也可以描述为给定一阶原点矩和二阶原点矩，这两个条件是等价的)则在所有满足这两个限制的概率分布中，熵最大的概率分布 $p(x|\mu, \sigma^2)$ 就是正态分布 $N(\mu, \sigma^2)$。

这个结论的推导数学上稍微有点复杂，不过如果已经猜到了给定限制条件下最大熵的分布是正态分布，要证明这个猜测却是很简单的，证明的思路如下给出。

考虑两个概率分布 $p(x), q(x)$。使用不等式 $\log x \le (x-1) $, 得

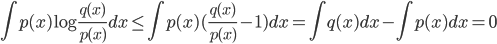
于是

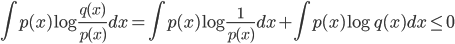
所以

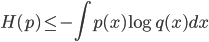
熟悉信息论的同学都知道，这个式子是信息论中的很著名的结论：一个概率分布的熵总是小于相对熵。上式要取等号只有取$q(x)=p(x)$。

对于 $p(x)$, 在给定的均值 $\mu$ 和方差 $\sigma^2$下, 我们取$q(x)=N(\mu, \sigma^2)$, 则可以得到

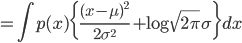
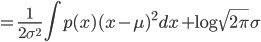
由于 $p(x)$ 的均值方差有如下限制

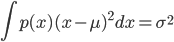
于是

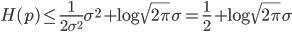
而当$p(x)=N(\mu, \sigma^2)$的时候，上式可以取到等号，这就证明了结论。

E.T.Jaynes 显然对正态分布具有这样的性质极为赞赏，因为这从信息论的角度证明了正态分布的优良性。而我们可以看到，熵的大小，取决于方差的大小。 这也容易理解， 因为正态分布的均值和密度函数的形状无关，而熵的大小反应概率分布中的信息量，显然和密度函数的形状相关，而正态分布的形状是由其方差决定的。

好的，风景欣赏暂时告一段落。所谓横看成岭侧成峰，远近高低各不同，正态分布给人们提供了多种欣赏角度和想象空间。法国菩萨级别的大数学家庞加莱对正态分布说过一段有意思的话，引用来作为这个小节的结束：

Physicists believe that the Gaussian law has been proved in mathematics while mathematicians think that it was experimentally established in physics.

— Henri Poincaré