
1. 神奇的Gamma函数
1.1 Gamma 函数诞生记
学高等数学的时候,我们都学习过如下一个长相有点奇特的Gamma函数
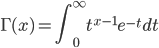
通过分部积分的方法,可以推导出这个函数有如下的递归性质
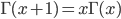
于是很容易证明,$\Gamma(x)$ 函数可以当成是阶乘在实数集上的延拓,具有如下性质
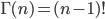
学习了Gamma 函数之后,多年以来我一直有两个疑问:
- 这个长得这么怪异的一个函数,数学家是如何找到的;
- 为何定义 $\Gamma$ 函数的时候,不使得这个函数的定义满足$\Gamma(n) = n! $ 而是 $\Gamma(n) = (n-1)! $
最近翻了一些资料,发现有不少文献资料介绍 Gamma 函数发现的历史,要说清楚它需要一定的数学推导,这儿只是简要的说一些主线。
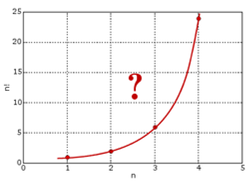
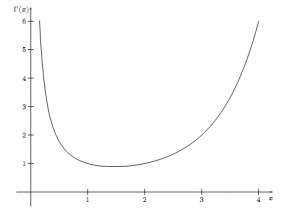
1728年,哥德巴赫在考虑数列插值的问题,通俗的说就是把数列的通项公式定义从整数集合延拓到实数集合,例如数列 $1,4,9,16,\cdots$ 可以用通项公式 $n^2$ 自然的表达,即便 $n$ 为实数的时候,这个通项公式也是良好定义的。直观的说也就是可以找到一条平滑的曲线$y=x^2$通过所有的整数点$(n,n^2)$,从而可以把定义在整数集上的公式延拓到实数集合。一天哥德巴赫开始处理阶乘序列 $1,2,6,24,120,720,\cdots$,我们可以计算 $2!,3!$, 是否可以计算 $2.5!$呢?我们把最初的一些 $(n,n!)$的点画在坐标轴上,确实可以看到,容易画出一条通过这些点的平滑曲线。
但是哥德巴赫无法解决阶乘往实数集上延拓的这个问题,于是写信请教尼古拉斯.贝努利和他的弟弟丹尼尔.贝努利,由于欧拉当时和丹尼尔.贝努利在一块,他也因此得知了这个问题。而欧拉于1729 年完美的解决了这个问题,由此导致了$\Gamma$ 函数的诞生,当时欧拉只有22岁。
事实上首先解决$n!$的插值计算问题的是丹尼尔.贝努利,他发现,
如果 $m,n$都是正整数,如果 $m \rightarrow \infty$,有
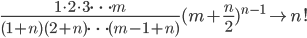
于是用这个无穷乘积的方式可以把$n!$的定义延拓到实数集合。例如,取 $n=2.5$, $m$ 足够大,基于上式就可以近似计算出 $2.5!$。
欧拉也偶然的发现 $n!$ 可以用如下的一个无穷乘积表达
\begin{equation}
\label{euler-series}
\Bigl[\Bigl(\frac{2}{1}\Bigr)^n\frac{1}{n+1}\Bigr]
\Bigl[\Bigl(\frac{3}{2}\Bigr)^n\frac{2}{n+2}\Bigr]
\Bigl[\Bigl(\frac{4}{3}\Bigr)^n\frac{3}{n+3}\Bigr] \cdots = n!
\quad (*)
\end{equation}
用极限形式,这个式子整理后可以写为
\begin{equation}
\label{euler-series2}
\lim_{m \rightarrow \infty} \frac{1\cdot 2\cdot 3 \cdots m}{(1+n)(2+n)\cdots (m+n)}(m+1)^{n} = n!
\quad (**)
\end{equation}
左边可以整理为
\begin{align*}
& \frac{1\cdot 2\cdot 3 \cdots m}{(1+n)(2+n)\cdots (m+n)}(m+1)^{n} \\
= & 1\cdot 2\cdot 3 \cdots n \cdot \frac{(n+1)(n+2)\cdots m}{(1+n)(2+n)\cdots m }
\cdot \frac{(m+1)^{n}}{(m+1)(m+2)\cdots (m+n)} \\
= & n! \frac{(m+1)^{n}}{(m+1)(m+2)\cdots (m+n)} \\
= & n!\prod_{k=1}^{n} \frac{m+1}{m+k} \rightarrow n! \qquad (m\rightarrow \infty)
\end{align*}
所以 (*)、(**)式都成立。
欧拉开始尝试从一些简单的例子开始做一些计算,看看是否有规律可循,欧拉极其擅长数学的观察与归纳。当 $n=1/2$ 的时候,带入(*)式计算,整理后可以得到
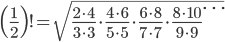
然而右边正好和著名的 Wallis 公式关联。Wallis 在1665年使用插值方法计算半圆曲线 $y = \sqrt{x(1-x)}$ 下的面积(也就是直径为1的半圆面积)的时候,得到关于$\pi$的如下结果,
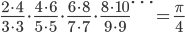
于是,欧拉利用 Wallis 公式得到了如下一个很漂亮的结果
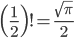
欧拉和高斯都是具有超凡直觉的数学家,但是欧拉和高斯的风格迥异。高斯是个老狐狸,数学上非常严谨,发表结果的时候却都把思考的痕迹抹去,只留下漂亮的结果,这招致了一些数学家对高斯的批评;而欧拉的风格不同,经常通过经验直觉做大胆的猜测,而他的文章中往往留下他如何做数学猜想的痕迹,而文章有的时候论证不够严谨。 拉普拉斯曾说过:”读读欧拉,他是所有人的老师。”波利亚在他的名著《数学与猜想》中也对欧拉做数学归纳和猜想的方式推崇备至。
欧拉看到 $ (\frac{1}{2})!$ 中居然有 $\pi$, 对数学家而言,有$\pi$ 的地方必然有和圆相关的积分。由此欧拉猜测 $n!$ 一定可以表达为某种积分形式,于是欧拉开始尝试把 $n!$ 表达为积分形式。虽然Wallis 的时代微积分还没有发明出来,Wallis 是使用插值的方式做推导计算的,但是Wallis 公式的推导过程基本上就是在处理积分 $\int_0^1 x^\frac{1}{2}(1-x)^\frac{1}{2}dx$,受 Wallis 的启发,欧拉开始考虑如下的一般形式的积分
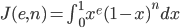
此处n 为正整数,$e$ 为正实数。利用分部积分方法,容易得到
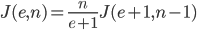
重复使用上述迭代公式,最终可以得到
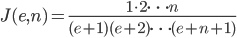
于是欧拉得到如下一个重要的式子
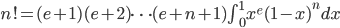
接下来,欧拉使用了一点计算技巧,取 $e=f/g$ 并且令 $f \rightarrow 1, g \rightarrow 0$,
然后对上式右边计算极限(极限计算的过程此处略去,推导不难,有兴趣的同学看后面的参考文献吧),于是欧拉得到如下简洁漂亮的结果:
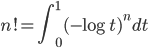
欧拉成功的把$n!$表达为了积分形式!如果我们做一个变换 $t=e^{-u}$,就可以得到我们常见的Gamma 函数形式
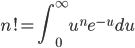
于是,利用上式把阶乘延拓到实数集上,我们就得到 Gamma 函数的一般形式
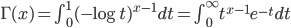
Gamma 函数找到了,我们来看看第二个问题,为何 Gamma 函数被定义为 $\Gamma(n)=(n-1)!$, 这看起来挺别扭的。如果我们稍微修正一下,把Gamma 函数定义中的 $t^{x-1}$ 替换为$t^x$
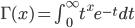
这不就可以使得 $\Gamma(n)=n!$了嘛。欧拉最早的Gamma函数定义还真是如上所示,选择了$\Gamma(n)=n!$,可是欧拉不知出于什么原因,后续修改了 Gamma 函数的定义,使得$\Gamma(n)=(n-1)!$。 而随后勒让德等数学家对Gamma 函数的进一步深入研究中,认可了这个定义,于是这个定义就成为了既成事实。有数学家猜测,一个可能的原因是欧拉研究了如下积分
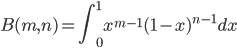
这个函数现在称为Beta 函数。如果Gamma 函数的定义选取满足 $\Gamma(n)=(n-1)!$, 那么有
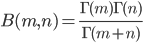
非常漂亮的对称形式。可是如果选取$\Gamma(n)=n!$ 的定义,令
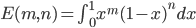
则有
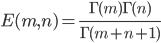
这个形式显然不如 $B(m,n)$优美,而数学家总是很在乎数学公式的美感的。
要了解更多的 Gamma 函数的历史,推荐阅读
- Philip J. Davis, Leonhard Euler's Integral: A Historical Profile of the Gamma Function
- Jacques Dutka, The Early History of the Factorial Function
- Detlef Gronnau, Why is the gamma function so as it is?


这位兄台是之前写“正态分布的前世今生”的那位?!
写得不错哦!
敢问是做什么的?
[回复]
rickjin 回复:
22 12 月, 2012 at 22:40
谢谢,我是中关村写代码的,偶尔为工程师做一些科普,如果对非工程师也有用,那是 side effect
[回复]
数学史还挺有意思
[回复]
看到后面beta函数,我想到数值分析课上,当时求积分,我正是构造这种二元函数找到的递归式。
[回复]
写得真不错,经常过来看看,很有收获
[回复]
在學Bayesian method,看這個真的很有幫助,謝謝!
[回复]
总结得蛮好的,而且LZ有心分享,真不错。
[回复]
我是一名研究生 最近在看机器学习方面的知识,偶然间发现了您的站点,写的很好。要多多向您学习。。。
[回复]
“当 n=1/2 的时候,带入(*)式计算,整理后可以得到”后面的式子是不是有问题?
[回复]
ken 回复:
2 10 月, 2017 at 20:58
确实有问题 少了2/1,wallis里是有的
[回复]
去年发现了这个网站,不知道现在还在维护吗?很有帮助的网站,今年打算在NLP领域好好研究一下,希望能得到作者指导。。。
[回复]