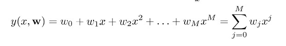PRML读书会第三章 Linear Models for Regression
主讲人 planktonli
planktonli(1027753147) 18:58:12
大家好，我负责给大家讲讲 PRML的第3讲 linear regression的内容，请大家多多指教，群主让我们每个主讲人介绍下自己，赫赫,我也说两句，我是 applied mathematics + computer science的，有问题大家可以直接指出，互相学习。大家有兴趣的话可以看看我的博客: http://t.qq.com/keepuphero/mine，当然我给大家推荐一个好朋友的，他对计算机发展还是很有心得的,他的网页http://www.zhizhihu.com/ 对machine learning的东西有深刻的了解。
好,下面言归正传，开讲第3章，第3章的名字是 linear regression，首先需要考虑的是: 为什么在讲完 introduction、probability distributions 之后就直讲 linear regression? machine learning的essence是什么?
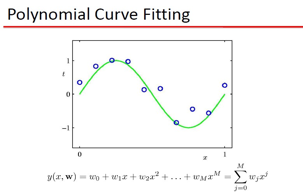
机器学习的本质问题: 我个人理解,就是通过数据集学习未知的最佳逼近函数，学习的 收敛性\界 等等都是描述这个学习到的function到底它的性能如何。但是,从数学角度出发,函数是多样的，线性\非线性\跳跃\连续\非光滑，你可以组合出无数的函数,那么这些函数就组成了函数空间，在这些函数中寻找到一个满足你要求的最佳逼近函数,无疑大海捞针。我们再来回顾下第一章的 曲线拟和问题：
需要逼近的函数是: 
，M阶的曲线函数可以逼近么？这是我们值得思考的问题。
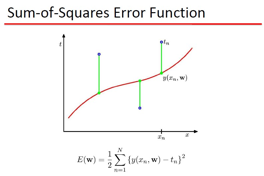
要曲线拟和, 那么拟和的标准是什么?这里用了2范数定义,也就是误差的欧式距离，当然,你可以用 L1,L无穷，等等了 ，只是objective不同罢了。现在的疑问是: 为什么要用Polynomial Fitting?有数学依据么，这里牵扯到 范函的问题，就是函数所张成的空间，举一个简单的例子，大家还都记得 talyor展式吧：
这表明 任意一个函数可以表示成 x的次方之和，也就是 任意一个函数 可以放到 
所张成的函数空间，如果是有限个基的话就称为欧式空间，无穷的话 就是 Hilbert空间，其实 傅里叶变换 也是这样的一个例子，既然已经明白了 任意函数可以用Polynomial Fitting，那么下面就是什么样的 Polynomial是最好的。
Wilbur_中博(1954123) 19:28:26
泰勒展开是局部的、x0周围的，而函数拟合是全局的，似乎不太一样吧？
planktonli(1027753147) 19:29:21
恩,泰勒展开是局部的，他是在 x0 点周围的一个 表达，函数拟合是全局的,我这里只是用一个简单的例子说明 函数表达的问题。
Wilbur_中博(1954123) 19:30:41
planktonli(1027753147) 19:31:03
其实,要真正解释这个问题是需要范函的东西的。
Wilbur_中博(1954123) 19:31:45
抱歉，打断了一下，因为我觉得这个问题留到讨论就不太好了，呵呵。了解了，请继续吧。
planktonli(1027753147) 19:31:51
由于大多数群友未学过这个课程,我只是想说下这个思想，呵呵,没事，讨论才能深刻理解问题，其实,wavelet这些,包括 kernel construcion这些东西都牵扯到 范函。
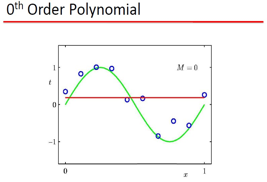
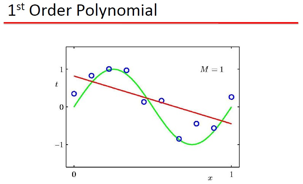
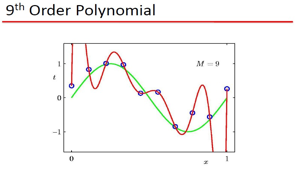
Bishop用上面这个例子说明 ：
1) 可以用 Polynomial Fitting 拟和 sin类的函数 2) 存在过拟和问题
而且这里的 Polynomial Fitting 是一个线性model， 这里Model是w的函数,w是线性的：
是线性的么，肯定不是，那么 让我们再来分析下 研究的问题
中的 x 是1维的
上面的X 变成了
，非常有意思的是: 维数升高了，同时这个model具有了表达非线性东西的
能力。这里的思想,可以说贯穿在 NN,SVM这些东西里，也就是说,线性的model如果应用得当的话,可以表达非线性的东西。与其在所有函数空间盲目的寻找,还不如从一个可行的简单model开始，这就是为什么Bishop在讲完基础后直接切入 Linear regression的原因，当然这个线性model怎么构造,是单层的 linear model,还是多层的 linear model 一直争论不休，BP否定了 perceptron 的model，SVM 否定了 BP model
现在deep learning 又质疑 SVM 的shallow model，或许这就是machine learning还能前进的动力。
让咱们再回来看看linear regression 的模型，这里从标准形式到扩展形式，也就是引入基函数后,Linear regression的模型可以表达非线性的东西了，因为基函数可能是非线性的：
基函数的形式，这些基函数都是非线性的：
在Gaussian 零均值情况下,Linear model从频率主义出发的MLE就是 Least square：
最小2乘的解就是广义逆矩阵乘输出值：
Gaussian的precision也可以计算出来：
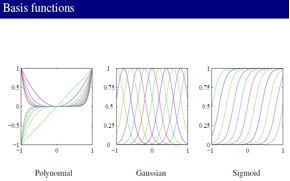
最小2乘的解可以看成到基张成空间的投影：
频率主义会导致 过拟和，加入正则,得到的最小2乘解：
正则参数对model结果的影响：
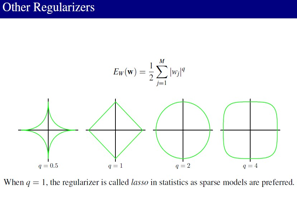
消除过拟和，正则的几何解释：
正则方法不同,就会出现很多model,例如 lasso, ridge regression。LASSO的解是稀疏的，例如:sparse coding,Compressed sensing 是从 L0--> L1sparse的问题，现在也很热的。
下面看 Bias-Variance Decoposition，正则就是在 训练数据的模型上加一个惩罚项，shrink 模型的参数,让它不要学习的太过，这里 
是对训练数据学习到的模型,
是学习到的参数的惩罚模型
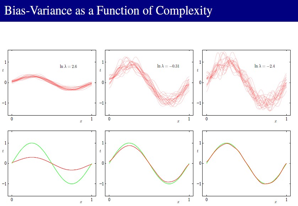
上面这么多PPT无非就是说，学习到的模型和真实的模型的期望由2部分组成：
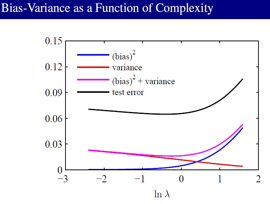
1--> Bias 2--> Variance。Bias表示的是学习到的模型和真实模型的偏离程度,Variance表示的是学习到的模型和它自己的期望的偏离程度。从这里可以看到正则项在控制 Bias 和 Variance：
Wilbur_中博(1954123) 20:33:07
这个是关键，呵呵
planktonli(1027753147) 20:33:25
Variance小的情况下,Bias就大，Variance大的情况下,Bias就小，我们就要tradeoff它们。
从这张图可以看到 Bias和 Variance的关系：
这个Bias-Variance Decoposition 其实没有太大的实用价值，它只能起一个指导作用。
下面看看 Bayesian Linear Regression：
从Bayesian出发,关注的不是参数的获取,而更多的是 新预测的值，通过后验均值可以得到 linear model和核函数的联系，当然也可以建立 gaussian process这些东西。
Wilbur_中博(1954123) 20:51:25
这里可以讲细一点么，如何建立联系？
planktonli(1027753147) 20:54:44
这里就可以看到了啊，看到了么，Wilbur?
Wilbur_中博(1954123) 20:57:24
在看
planktonli(1027753147) 20:58:08
如果共扼先验是 0均值情况下,linear model就可以变成 kernel了：
最后讲了bayesain model比较：
选择最大信任的model来作为模型选择，而非用交叉验证，信任近似：
固定基存在缺陷为 NN,SVM做铺垫，NN,SVM都是变化基，BP是梯度下降error,固定基，RBF是聚类寻找基，SVM是2次凸优化寻找基。好了,就讲到这里吧，肯定还有讲的不对,或者不足的地方，请大家一起讨论和补充，谢谢。
============================讨论===============================
Wilbur_中博(1954123) 21:08:29
RBF不是固定径向基找系数的么，SVM也是固定基的吧，这里寻找基是什么意思？
planktonli(1027753147) 21:09:01
SVM是寻找那些 系数不为0的作为基，RBF,我说的是RBF神经网络，不是RBF基函数，呵呵
Wilbur_中博(1954123) 21:11:07
嗯，但咱们现在这一章，比如多项式基，也可以说是寻找系数不为0的x^k吧，SVM也仍然是固定了某一种核，比如多项式核或者高斯核。嗯，我知道是说RBF网络。
planktonli(1027753147) 21:11:40
恩,可以这么说
Wilbur_中博(1954123) 21:12:35
还有就是，固定一组基的话，也有很多选择，有多项式、也有高斯、logisitic等等，那我们应该怎么选择用什么基去做回归呢？这一章讲得大多都是有了基以后怎么选择w，但怎么选择基这一点有没有什么说法。
planktonli(1027753147) 21:13:37
我说的固定指的是,SVM不知道基是谁，而是通过优化获取的。
Wilbur_中博(1954123) 21:13:41
或者小波傅里叶什么的。。好多基
planktonli(1027753147) 21:14:03
这里提出了固定基的问题，基的选择要看样本的几何形状，一般都是 选择 gaussian，当然也可以一个个测试着弄。
Wilbur_中博(1954123) 21:15:55
SVM里有个叫multiple kernel learning的，感觉像是更广泛的变化基的解决方案。嗯，就是说大多是经验性的是吧，选基这个还是蛮有趣的，我觉得。
planktonli(1027753147) 21:16:45
恩,MK是多个kernel的组合，尝试用多个几何形状的kernl去寻找一个更power的。
Wilbur_中博(1954123) 21:17:05
嗯，呵呵
planktonli(1027753147) 21:17:16
恩,kernel construction是ML的主要研究内容之一
Wilbur_中博(1954123) 21:18:14
好的，我没什么问题了，谢谢，以后多交流。看其他朋友还有什么问题。
planktonli(1027753147) 21:50:29
本次的讲义有些内容是群共享里的 Linear1.pdf
下次的linear classification主要讲的内容在群共享中为Linear2.pdf
注：PRML读书会系列文章由 @Nietzsche_复杂网络机器学习 同学授权发布，转载请注明原作者和相关的主讲人，谢谢。
PRML读书会讲稿PDF版本以及更多资源下载地址：http://vdisk.weibo.com/u/1841149974
本文链接地址：https://www.52nlp.cn/prml读书会第三章-linear-models-for-regression
http://credit-n.ru/zaymyi-next.html