
在数据量越来越大的今天,
word2vec是通过字词的共现关系来学习字词的向量表示,Graph Embeding的思想类似于word2vec,通过图中节点与节点的共现关系来学习节点的向量表示,构成文本序列从而计算相互关联出现的词的概率,从而计算词向量表示文本。那么在图模型中的关键的问题就是如何来描述节点与节点的共现关系,于是方法是利用DeepWalk来采样这样的文本序列,通过随机游走(RandomWalk)的方式在图中进行节点采样,从而就能够输入序列计算图的向量表示。所以deepwalk算法核心的步骤就是两步:
- RandomWalk
- Skip-Gram
RandomWalk是一种可重复访问已访问节点的深度优先遍历算法。给定当前访问起始节点,从其邻居中随机采样节点作为下一个访问节点,重复此过程,直到访问序列长度满足预设条件。

算法过程就是输入一个图,输出节点表示的矩阵,简单对步骤进行解析:
- 初始化:从 $\mathcal{U}^{|V| \times d}$ 样本空间中采样,embedding的大小为 $d$
- 构建一棵二叉树Hierarchical Softmax
- 开始做 $\gamma$ 步的随机游走,这里的 $\gamma$ 是初始化好的超参数
- 打乱采样得到的节点
- 这个循环是开始以每个节点为根节点开始做长度为 $t$ 的随机游走,这里的 $t$ 为初始化的超参数。然后按窗口 $w$ 进行SkipGram学习文本序列
SkipGram
一般提到word2vec有两种主要的算法,Cbow和Skip-Gram,都是在统计语言模型的基础上计算一个词在文本中出现的概率用来作为这个词的表示向量,于是优化目标就是最大化$Pr(w_n|w_0,w_1,...,w_{n-1})$ 。 $w$ 表示的就是词。
SkipGram就是用当前词来预测上下文。丢掉了词序并且不考虑与当前词的距离。优化目标是最大化同一个句子中同时出现的词的共现概率:
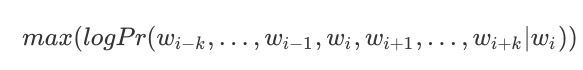
预测给到的词从整个词表vocabulary中选择,因此在输出的时候会计算softmax进行选择,维度为 $|V|$ ,计算的维度会非常大,因此采用Hierarchical Softmax来构建二叉树进行选择,每个词就只需要计算 $log_2^{|V|}$ 次。
Node2Vec
node2vec依然采用的是随机游走的方式获取顶点的临近顶点序列,但不同的是node2vec采用的是一种有偏的随机游走。给定当前顶点 $v$,访问下一个顶点的概率是:
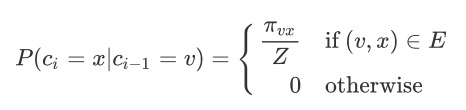
$\pi{vx}$ 是顶点 $v$ 到顶点 $x$ 之间的转移概率, $Z$ 是归一化参数。 node2vec引入两个超参数 $p$ 和 $q$ 来控制随机游走的策略,假设当前随机游走经过边 $(v, x) $ 到达顶点 $t$ ,设 $\pi{vx}=\alpha{pq}(t, x)\cdot w{vx}$ , $w_{vx}$ 是顶点 $v$ 和 $x$ 之间的边权。
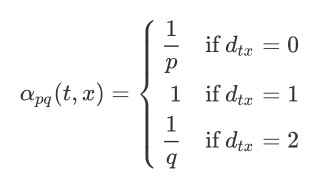
$d{tx}$ 为顶点 $t$ 和顶点 $x$ 之间的最短路径距离。 参数$p$和参数$q$的意义:控制重复访问刚刚访问过的顶点的概率。$p$作用于$d{tx}=0$,表达的意义就是顶点$x$就是访问当前顶点$v$之前刚刚访问过的顶点。如果$p$较高,则访问刚刚访问过的顶点的概率会变低,反之变高。$q$控制着游走是向外还是向内,如果$q>1$,随机游走倾向于访问和节点$t$相接近的顶点(类似于$BFS$)。如果$q<1$,则倾向于访问远离$t$的顶点(类似于$DFS$)。
Graph Convolutional Network
Graph Embedding的意义就在于能够利用图结构处理非结构化数据,因此在cv和nlp领域能够更进一步结合先验知识进行特征学习,因此是深度学习领域的重要发展方向。 定义图$G=(V,E)$,$V$为节点的集合,$E$为边的集合,对于每个节点$i$, 均有其特征$x_i$,特征矩阵可以用$X_{N*D}$来表示,其中$N$表示节点数,$D$表示每个节点的特征编码尺寸,在nlp应用中就是embedding_size。对于图的理解有一个经典的思想:
图中的每个结点无时无刻不因为邻居和更远的点的影响而在改变着自己的状态直到最终的平衡,关系越亲近的邻居影响越大。
实际上从邻居节点获取信息的思想在很多领域都有应用,例如:word2vec和pagerank。很多参考的理解描述了更加细节的数学原理:从傅立叶变换到拉普拉斯算子到拉普拉斯矩阵。很难理解。

公式显示为源码,比如$x_i$,建议修复。
[回复]