Coursera公开课笔记: 斯坦福大学机器学习第二课“单变量线性回归(Linear regression with one variable)”

1) Model representation(模型表示)

回到第一课中的房屋价格预测问题， 首先它是一个有监督学习的问题（对于每个样本的输入，都有正确的输出或者答案），同时它也是一个回归问题（预测一个实值输出）。

训练集表示如下：

其中：

m = 训练样本的数目

x's = “输入”变量，也称之为特征

y's = “输出”变量，也称之为“目标”变量

对于房价预测问题，学习过程可用下图表示：

其中x代表房屋的大小，y代表预测的价格，h(hypothesis)将输入变量 x 映射到输出变量 y，如何表示h?

事实上Hypothesis可以表示成如下形式：

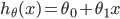
简写为 h(x)，也就是带一个变量的线性回归或者单变量线性回归问题。

2) Cost function(代价函数，成本函数)

对于Hypothesis: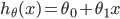 

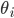为参数

如何求?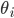

构想： 对于训练集(x, y)，选取参数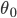, 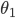使得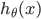尽可能的接近y。

如何做呢？一种做法就是求训练集的平方误差函数（squared error function），Cost Function可表示为:

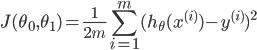
并且选取合适的参数使其最小化，数学表示如下：

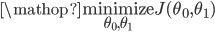
3) Cost function intuition I(直观解释1)

直观来看，线性回归主要包括如下四大部分，分别是Hypothesis, Parameters, Cost Function, Goal:

这里作者给出了一个简化版的Cost function解释，也就是令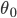为0：

然后令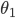分别取1、0.5、-0.5等值，同步对比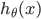和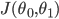在二维坐标系中的变化情况，具体可参考原PPT中的对比图，很直观。

4) Cost function intuition II(直观解释2)

回顾线性回归的四个部分，这一次不在对Cost Function做简化处理，这个时候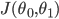的图形是一个三维图或者一个等高线图，具体可参考原课件。

可以发现，当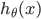的直线越来越接近样本点时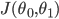，在等高线的图中的点越来越接近最小值的位置。

5) Gradient descent(梯度下降)

应用的场景之一-最小值问题：

对于一些函数，例如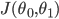

目标: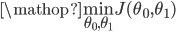 

方法的框架:

1、给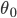, 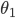一个初始值，例如都等于0

2、每次改变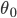, 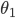的时候都保持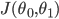递减，直到达到一个我们满意的最小值；

对于任一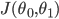 , 初始位置不同，最终达到的极小值点也不同，例如以下两个例子：

梯度下降算法：

重复下面的公式直到收敛：

举例：

参数正确的更新过程如下（同步更新）：

错误的更新过程如下：

6) Gradient descent intuition(梯度下降直观解释)

举例，对于一个简化的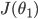来说，无论抛物线的左边还是右边，在梯度下降算法下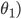，都是保持正确的方向（递增或递减）

对于learning rate(又称为步长)来说:

如果过小，梯度下降可能很慢；如果过大，梯度下降有可能“迈过”（overshoot）最小点，并且有可能收敛失败，并且产生“分歧”(diverge)

梯度下降可以使函数收敛到一个局部最小值，特别对于learning rate 是固定值的时候：

当函数接近局部最小值的时候，梯度下降法将自动的采取“小步子”， 所以没有必要随着时间的推移减小learning rate.

关于梯度下降算法，可以参考维基百科的介绍： http://zh.wikipedia.org/wiki/%E6%A2%AF%E5%BA%A6%E4%B8%8B%E9%99%8D%E6%B3%95

7) Gradient descent for linear regression(应用于线性回归的的梯度下降算法)

梯度下降算法：

线性回归模型：

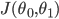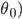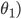对于, 求导，得：

在梯度下降算法中进行替换，就得到单变量线性回归梯度下降算法：

详细的图形举例请参考官方PPT，主要是在等高线图举例梯度下降的收敛过程，逐步逼近最小值点，其中一幅图说明：线性回归函数是凸函数(convex function)，具有碗状（bowl shape)。

总结： 这里的梯度下降算法也称为"Batch" 梯度下降: 梯度下降的每一步都使用了所有的训练样本。

本文链接地址：Coursera公开课笔记: 斯坦福大学机器学习第二课“单变量线性回归(Linear regression with one variable)”