六、维特比算法（Viterbi Algorithm）
维特比算法定义(Viterbi algorithm definition)
1、维特比算法的形式化定义
维特比算法可以形式化的概括为：
对于每一个i，i = 1，... ，n，令：
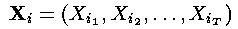
——这一步是通过隐藏状态的初始概率和相应的观察概率之积计算了t=1时刻的局部概率。
对于t=2，...，T和i=1，...，n,令：
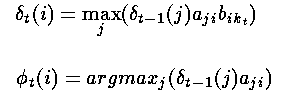
——这样就确定了到达下一个状态的最可能路径，并对如何到达下一个状态做了记录。具体来说首先通过考察所有的转移概率与上一步获得的最大的局部概率之积，然后记录下其中最大的一个，同时也包含了上一步触发此概率的状态。
令：
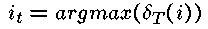
——这样就确定了系统完成时(t=T)最可能的隐藏状态。
对于t=T-1，...，1
令：
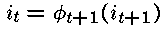
——这样就可以按最可能的状态路径在整个网格回溯。回溯完成时，对于观察序列来说，序列i1 ... iT就是生成此观察序列的最可能的隐藏状态序列。
2.计算单独的
's和
's
维特比算法中的局部概率's的计算与前向算法中的局部概率
's的很相似。下面这幅图表显示了's和's的计算细节，可以对比一下前向算法3中的计算局部概率's的那幅图表：
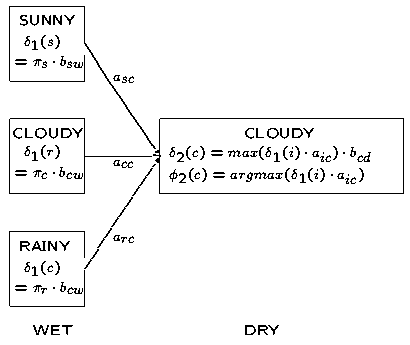
（注：本图及前向算法3中的相似图存在问题，具体请见前向算法3文后评论，非常感谢读者YaseenTA的指正）
唯一不同的是前向算法中计算局部概率's时的求和符号（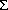
）在维特比算法中计算局部概率's时被替换为max——这一个重要的不同也说明了在维特比算法中我们选择的是到达当前状态的最可能路径，而不是总的概率。我们在维特比算法中维护了一个“反向指针”记录了到达当前状态的最佳路径，即在计算's时通过argmax运算符获得。
总结(Summary)
对于一个特定的隐马尔科夫模型，维特比算法被用来寻找生成一个观察序列的最可能的隐藏状态序列。我们利用概率的时间不变性，通过避免计算网格中每一条路径的概率来降低问题的复杂度。维特比算法对于每一个状态(t>1)都保存了一个反向指针()，并在每一个状态中存储了一个局部概率()。
局部概率是由反向指针指示的路径到达某个状态的概率。
当t=T时，维特比算法所到达的这些终止状态的局部概率's是按照最优（最可能）的路径到达该状态的概率。因此，选择其中最大的一个，并回溯找出所隐藏的状态路径，就是这个问题的最好答案。
关于维特比算法，需要着重强调的一点是它不是简单的对于某个给定的时间点选择最可能的隐藏状态，而是基于全局序列做决策——因此，如果在观察序列中有一个“非寻常”的事件发生，对于维特比算法的结果也影响不大。
这在语音处理中是特别有价值的，譬如当某个单词发音的一个中间音素出现失真或丢失的情况时，该单词也可以被识别出来。
未完待续：维特比算法5
本文翻译自：http://www.comp.leeds.ac.uk/roger/HiddenMarkovModels/html_dev/main.html
部分翻译参考：隐马尔科夫模型HMM自学
转载请注明出处“我爱自然语言处理”：www.52nlp.cn
本文链接地址：https://www.52nlp.cn/hmm-learn-best-practices-six-viterbi-algorithm-4
——这样就确定了系统完成时(t=T)最可能的隐藏状态。
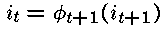
对于t=T-1，…，1
令：
——这样就可以按最可能的状态路径在整个网格回溯。回溯完成时，对于观察序列来说，序列i1 … iT就是生成此观察序列的最可能的隐藏状态序列。
这里面公式为什么是t+1，而不是t-1，回溯应该是减1吧，我可能没明白原理，请再详细说下，谢谢。
[回复]
admin 回复:
16 9 月, 2009 at 23:37
正因为是回溯，所以才是t+1,譬如当t=T-1时，
(T)(iT)了。
t+1指的是T时刻，而t指的就是T-1时刻，这个公式就转换为：
i(T-1) =
如果是t-1的话，就变成了从T-2到T-1时刻，不是回溯，而是从前向后的计算了。
[回复]
明白了，十分感谢。
[回复]
我觉
δt(i)=max[δt-1(i)*aji]*bikt
否则
正向经过的路径可能与反向指针指向的路径不一致
[回复]
52nlp 回复:
14 3 月, 2010 at 12:35
感觉您这个公式有问题，
δt(i)=max[δt-1(j)*aji]*bikt
中j应视作一个变量，from 1 to N中的任何一个。
[回复]
我有个疑问：您看在计算反响指针的时候，并没有在max中包含bik（发射矩阵），这样会不会回溯得到的路径并不是实际计算得到的最大概率的那个路径呢？同时，图中的局部概率计算公式和本文开始给出的局部概率公式也不一样。
[回复]
yky 回复:
6 2 月, 2013 at 10:28
我也觉得这个公式有问题。应该与求最大局部概率时max括号内一致。查看了wiki，也是在argmax中包含bik的。http://en.wikipedia.org/wiki/Viterbi_algorithm
[回复]
Eclipse 回复:
22 4 月, 2014 at 19:50
我是这么理解的，因为指针回溯的目的是辨识观测序列的噪音，如果这个式子中考虑了观测序列对概率的影响是没有办法滤除噪音的。
博主在前一小节中作过解释，这个指针的作用仅仅是考察前一步最有可能的状态。比如day3观测值是Dry，但有可能计算出来的序列中day3是Rainy，显然Pr(Dry|Rain)是很小的，那么观测值是不是有噪音呢，可以结合前一天的天气辅助判断(回溯)。
(算法还没看完，不知道到底是不是这么用的)
[回复]
Eclipse 回复:
22 4 月, 2014 at 20:21
又仔细看了一遍算法，回溯的公式中虽然没有包含t时刻的b(ik)，但是可以看出对t-1时刻不同的状态来说b(ik,t)只是不变的系数。而且指针回溯只返回索引，结果不受影响，回溯的隐藏状态序列和局部概率最大的序列是对应的。
但是这样的话滤除噪音的原理是什么呢？
是包含的，只是它不影响argmax的求解，所以被去掉了，还是建议再仔细读读其他关于HMM的资料，不能靠这个翻译解决所有问题。这个图是有问题的，已经有读者指出了，在下面有注明。事实上，英文原文里还有一些小问题，是在翻译的过程中发现的。
[回复]
https://www.52nlp.cn/images/6.2.1_a.gif
初始化为什么会把1,...,T的观察概率都计算进去？
我感觉是对于i，i=1,...,n,t=1时
X={X11，X21,...,Xn1}
[回复]
52nlp 回复:
19 5 月, 2010 at 23:31
这里可能没有表述清楚，不过你的理解有误，Xi1代表的是初始化时的情况，具体可参加前一节。
[回复]
那幅图，是不是画错了？前向算法的图也一样。
CLOUDY
δ1(c) = π[c]*b[cw]
RAINY
δ1(r) = π[r]*b[rw]
[回复]
Tsing 回复:
13 12 月, 2010 at 16:13
额。。看到标注了。抱歉刚才没注意
[回复]
52nlp 回复:
14 12 月, 2010 at 08:38
能看出图有错的读者都是很认真的，赞！
[回复]
嗯 找出最大，并且记住最大来自于何处
[回复]
谢谢博主，理解了很多
[回复]