
上一章我们详细介绍了小样本做文本分类中的胶囊网络,那么这一章我们就来看看RNN(循环神经网络)。大神们准备好了吗,我们要发车了~
首先就是我们为什么需要RNN?
举个简单的例子,最近娱乐圈顶流明星吴亦凡又出新瓜,大家都吃了咩?(反正小编吃的很饱哈)那么就以我 吃 瓜为例,三个单词标注词性为 我/nn 吃/v 瓜/nn。
那么这个任务的输入就是:
我 吃 瓜 (已经分词好的句子)
这个任务的输出是:
我/nn 吃/v 瓜/nn(词性标注好的句子)
很明显,一个句子中,前一个单词其实对于当前单词的词性预测是有很大影响的,比如预测“瓜”的时候,由于前面的吃是一个动词,那么很显然“瓜”作为名词的概率就会远大于动词的概率,因为动词后面接名词很常见,而动词后面接动词很少见。
所以为了更好的处理序列的信息,解决一些这样类似的问题,我们的RNN就诞生了。
rnn的结构和原理
看完初步的概念我们来深入一点看看RNN的结构和原理。
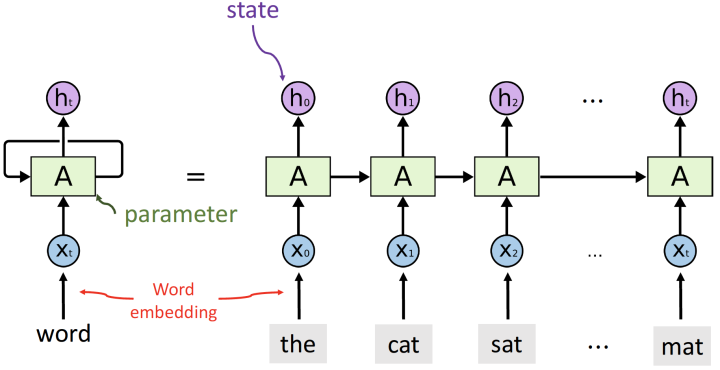
刚开始看到这幅图的同学会不会有一点懵懵?没关系,我们来带着解释一遍~
首先通过这副图,就能明白RNN的意义就是每个输出的状态都只由前一时刻的状态和当前时刻的输入来决定。从等式左边的一个环绕箭头就能明白参数是共享的。
一个序列的每个词就是每个时间步,每个词都会对应得到一个hidden_state,并将这个隐藏层状态输入下一个时间步。
最终会得到output和hidden,output是每一步运算的输出,因此output=(seqence_len, batch_size, hidden_size)。hidden_state是每一步的输出,当然有参数来控制可以取最后一步的输出,所以RNN中一般output=hidden。
lstm的结构和原理
聊完一圈RNN之后,我们来看看它的变种兄弟-LSTM吧!
别慌,我说的不是变种成僵尸的那种东东,Lstm为长短期记忆,是在RNN的基础上引入了细胞状态,根据细胞状态可决定哪些状态应该保留下来,哪些状态应该被遗忘,可以在一定程度上解决梯度消失问题。
那么为了能够学习序列关系的长期依赖,Lstm的输出和rnn一样都包含output和hidden,除此之外还有一个cell_state,这个就是学习序列信息lstm与rnn的差异。
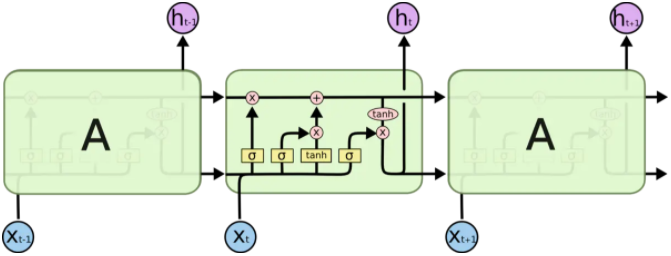
在lstm里面理解的就是用“门”结构,来选择信息通过,关键是用了$sigmoid(\cdot)$函数来区分趋于0的和趋于1的特征数据。
Lstm将使用三种门(不是那个日常开的那个门喔~)来保持和控制信息,分别为输入门、遗忘门、输出门。
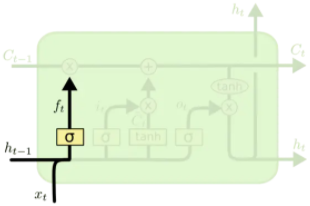
遗忘门:通过$f_t=\sigma(W_f \cdot[h_{t-1},x_t] + b_f)$ 来判断隐藏层信息的取舍。
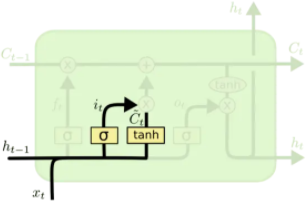
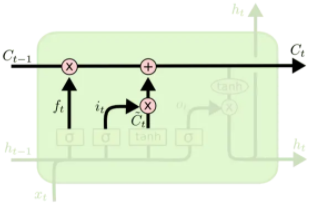
输入门:
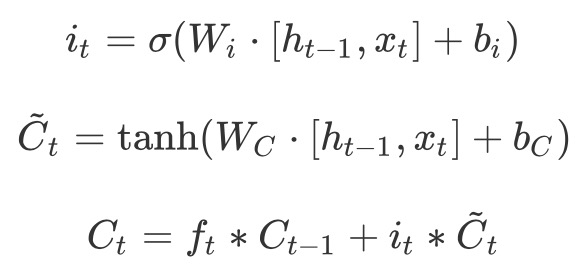
通过$\tanh(\cdot)$,来将隐藏层状态映射到(-1,1)最后来更新$C_{t-1}$ 到$C_t $
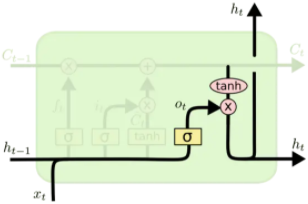
输出门:
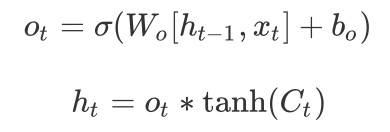
会发现$f_t、i_t、o_t$的构成是一致的。但是通过不同的权重来学习。因此优化lstm是将遗忘门和输入门合并成了一个更新门,这就是GRU:
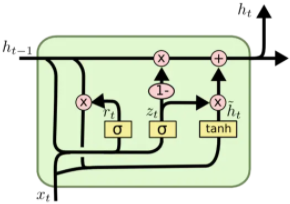
可以理解为主要分为两部分,第一部分:
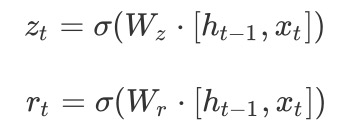
$z_t$表示更新向量,$r_t$表示重置向量,于是在接下来就能够考虑$r_t$与$h_{t-1}$的相关性来去对部分数据进行重置,也就相当于舍弃。实现遗忘门的效果。
第二部分:
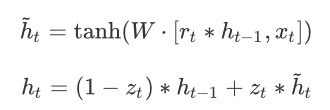
很好理解,就可以通过筛选得到的有效的隐藏层信息$\tilde{h}t$和更新向量来获取最终的输出结果$(1-z_t) * h{t-1}$表示对当前一时刻隐藏层状态选择性“遗忘”。$z_t * \tilde{h}_t$就表示对当前序列信息的“记忆”。
sequence-to-sequence的结构和原理
也叫做Encoder-Decoder结构,在encoder和decoder中也都是用序列模型,就是将数据先encode成一个上下文向量context vector,这个context vector可以是1)最后一个隐藏层状态,2)可以是完整的隐藏层输出,3)也可以是对隐藏层输出做激活或者线性变换之后的输出。
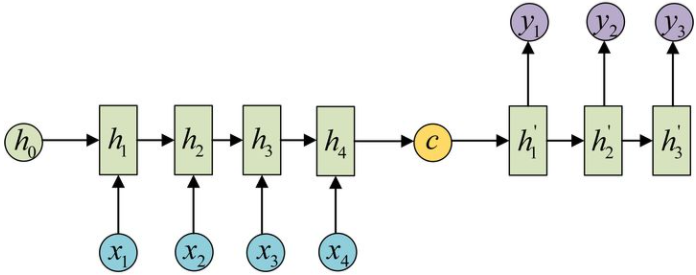
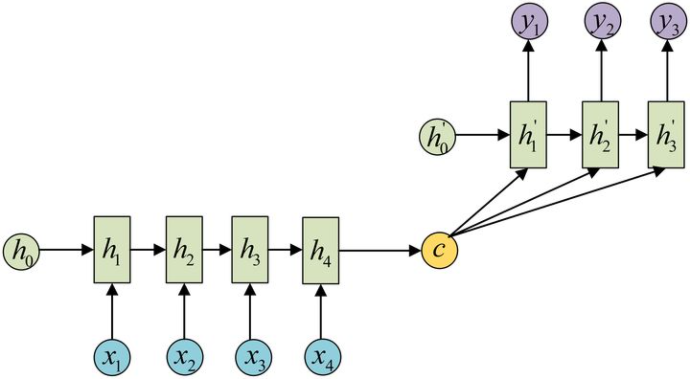
之后在decoder中,将context vector作为前一时刻初始化的状态输入从而将语义按监督信息的需要解码。或者将context vector作为decoder每一个时间步的输入。因此会发现seq2seq并不限制输入和输出的序列长度,这就表示应用范围可以很广。
Attention
我们会发现context vector并不能够包含长句的所有信息,或者说会造成信息的丢失,因此attention机制就是能够向decoder的每一个时间步输入不同的文本信息,提升语义的理解能力。
因为lstm会得到完整的包含每一个时间步的输出得到的ouput和hidden,因此$h_i$和$C_j$的相关性就能够表示在decode第$j$步序列时最关心的文本是那一步的 $h_i $,用 $\alpha_{ij}$来表示。
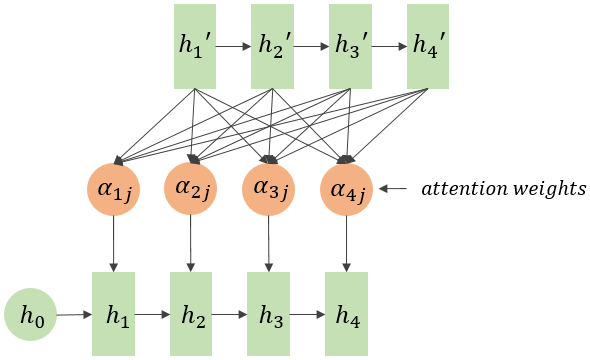
每一个encoder的hidden单元和每一个decoder的hidden单元做点乘,得到每两个单元之间的相关性,在lstm/rnn之后用attention就是计算hidden和ouput的每个单元之间的相关性,然后做一步$softmax$得到encoder的hidden或者说是lstm的hidden每个单元的attention weights。因此:Attention 无非就是这三个公式:
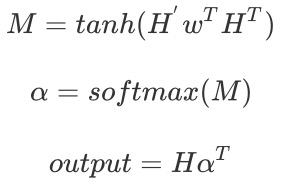
从常规的(Q,K,V)的角度来理解,可以如图所示:
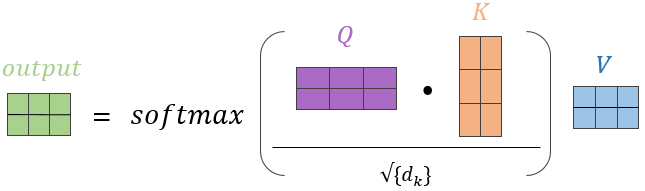
在Attention中$Q$和$K$分别是hidden和output,同样的$V$也是ouput,在self-attention中Q=K=V,并且$\sqrt{d_k}$有些情况下是不会加在attention过程中的。
-scaled.jpg)