七、前向-后向算法(Forward-backward algorithm)
隐马尔科夫模型（HMM）的三个基本问题中，第三个HMM参数学习的问题是最难的，因为对于给定的观察序列O，没有任何一种方法可以精确地找到一组最优的隐马尔科夫模型参数（A、B、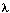
)最大。因而，学者们退而求其次，不能使P(O|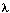)全局最优，就寻求使其局部最优（最大化）的解决方法，而前向-后向算法（又称之为Baum-Welch算法）就成了隐马尔科夫模型学习问题的一种替代（近似）解决方法。
我们首先定义两个变量。给定观察序列O及隐马尔科夫模型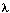，定义t时刻位于隐藏状态Si的概率变量为：
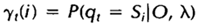
回顾一下第二节中关于前向变量at(i)及后向变量Bt(i)的定义，我们可以很容易地将上式用前向、后向变量表示为：
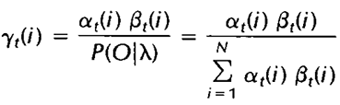
其中分母的作用是确保：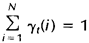
给定观察序列O及隐马尔科夫模型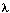，定义t时刻位于隐藏状态Si及t+1时刻位于隐藏状态Sj的概率变量为：
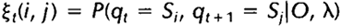
该变量在网格中所代表的关系如下图所示：
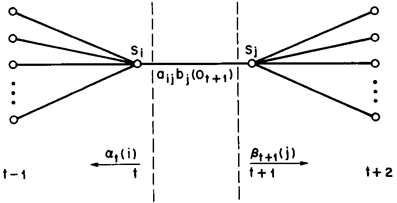
同样，该变量也可以由前向、后向变量表示：
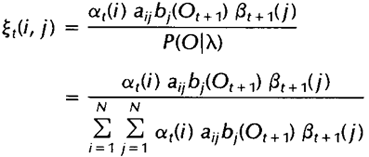
而上述定义的两个变量间也存在着如下关系：
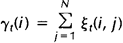
如果对于时间轴t上的所有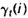
相加，我们可以得到一个总和，它可以被解释为从其他隐藏状态访问Si的期望值（网格中的所有时间的期望），或者，如果我们求和时不包括时间轴上的t=T时刻，那么它可以被解释为从隐藏状态Si出发的状态转移期望值。相似地，如果对
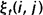在时间轴t上求和（从t=1到t=T-1），那么该和可以被解释为从状态Si到状态Sj的状态转移期望值。即：
未完待续：前向-后向算法5
注：原创文章，转载请注明出处“我爱自然语言处理”：www.52nlp.cn
本文链接地址：https://www.52nlp.cn/hmm-learn-best-practices-seven-forward-backward-algorithm-4
你好，问个局外的问题，你这个是免费的空间吗？是谁提供的？
[回复]
是免费的，http://www.exwebs.com/ 提供的。
[回复]
写的超好的说 但不是很明白这一段 如果对于时间轴t上的所有相加，我们可以得到一个总和，它可以被解释为从其他隐藏状态访问Si的期望值（网格中的所有时间的期望），或者，如果我们求和时不包括时间轴上的t=T时刻，那么它可以被解释为从隐藏状态Si出发的状态转移期望值。相似地，如果对在时间轴t上求和（从t=1到t=T-1），那么该和可以被解释为从状态Si到状态Sj的状态转移期望值。 为什么是期望值而不是概率呢？？？？
[回复]
yaya 回复:
19 10 月, 2015 at 10:47
公式看不太懂
[回复]
Pikoyo 回复:
7 5 月, 2020 at 18:22
您好，我也有这个困惑，请问您解决了吗？
[回复]
您好，请教您一个问题：在给定观察序列O的情况下，用B-W算法寻求一个λ使得P(O|λ)最大，这里的P(O|λ)与用迭代好了的λ使用前向算法计算的P(O|λ)是一致的吗？
[回复]
请问下,这个所谓的观察序列O 是不是就是学习的样本空间了呢?如果是的话,那么O应该包括了显性的输出和隐性的状态,对吗???
[回复]
您好，关于变量gamma用前向、后向变量表示的公式中，分母的累加式中的i与分子的i应该不是同一个含义吧？是否会引起歧义呢？
[回复]