七、前向-后向算法(Forward-backward algorithm)
要理解前向-后向算法，首先需要了解两个算法：后向算法和EM算法。后向算法是必须的，因为前向-后向算法就是利用了前向算法与后向算法中的变量因子，其得名也因于此；而EM算法不是必须的，不过由于前向-后向算法是EM算法的一个特例，因此了解一下EM算法也是有好处的，说实话，对于EM算法，我也是云里雾里的。好了，废话少说，我们先谈谈后向算法。
1、后向算法（Backward algorithm）
其实如果理解了前向算法，后向算法也是比较好理解的，这里首先重新定义一下前向算法中的局部概率at(i)，称其为前向变量，这也是为前向-后向算法做点准备：
相似地，我们也可以定义一个后向变量Bt(i)（同样可以理解为一个局部概率）：
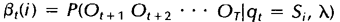
后向变量(局部概率)表示的是已知隐马尔科夫模型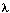
及t时刻位于隐藏状态Si这一事实，从t+1时刻到终止时刻的局部观察序列的概率。同样与前向算法相似，我们可以从后向前（故称之为后向算法）递归地计算后向变量：
1）初始化，令t=T时刻所有状态的后向变量为1：
2）归纳，递归计算每个时间点，t=T-1,T-2,…,1时的后向变量：
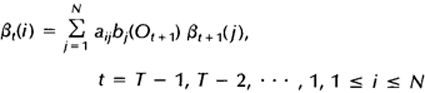
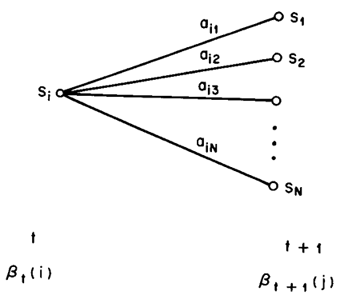
这样就可以计算每个时间点上所有的隐藏状态所对应的后向变量，如果需要利用后向算法计算观察序列的概率，只需将t=1时刻的后向变量（局部概率）相加即可。下图显示的是t+1时刻与t时刻的后向变量之间的关系：
上述主要参考自HMM经典论文《A tutorial on Hidden Markov Models and selected applications in speech recognition》。下面我们给出利用后向算法计算观察序列概率的程序示例，这个程序仍然来自于UMDHMM。
后向算法程序示例如下（在backward.c中):
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 | void Backward(HMM *phmm, int T, int *O, double **beta, double *pprob) { int i, j; /* state indices */ int t; /* time index */ double sum; /* 1. Initialization */ for (i = 1; i <= phmm->N; i++) beta[T][i] = 1.0; /* 2. Induction */ for (t = T - 1; t >= 1; t--) { for (i = 1; i <= phmm->N; i++) { sum = 0.0; for (j = 1; j <= phmm->N; j++) sum += phmm->A[i][j] * (phmm->B[j][O[t+1]])*beta[t+1][j]; beta[t][i] = sum; } } /* 3. Termination */ *pprob = 0.0; for (i = 1; i <= phmm->N; i++) *pprob += beta[1][i]; } |
好了，后向算法就到此为止了，下一节我们粗略的谈谈EM算法。
未完待续：前向-后向算法3
注：原创文章，转载请注明出处“我爱自然语言处理”：www.52nlp.cn
本文链接地址：http://www.52nlp.cn/hmm-learn-best-practices-seven-forward-backward-algorithm-2
相关文章:
博主您好，文中提到：“后向变量(局部概率)表示的是已知隐马尔科夫模型lamda及t时刻位于隐藏状态Si这一事实，从t+1时刻到终止时刻的局部观察序列的概率”。可是HMM假设观测值Ot只与当前的隐状态qt = Si有关。为什么后向变量Bt(i)可以定义成这样的一个条件概率呢？
[回复]
emnlp 回复:
五月 9th, 2011 at 19:40
当前的观测值确实只和当前的隐含状态相关，但是当前的隐含状态，却和其之前的隐含状态（观测值）相关了，… ，直到你逆推到t=0。如此以来，你想计算某时刻观测概率，那就得从头t=0一遍。。。 这里讲的几种算法，是提供如何有效计算这种概率的方法。
要不你先看看 前面的前向算法？
[回复]